How lexers (e.g. from LEX) and parsers (e.g. from YACC or JAVACC) work

How lexers and parsers work

Lexers - Finite State Automata (FSA)

Lexers are also known as scanners. LEX converts each set of regular expressions into a Deterministic FSA (DFSA) e.g. for a(b|c)d*e+

which has states 0 to 3, where state 0 is the initial state and state 3 is an accept state that indicates a possible end of the pattern.

LEX implements this by creating a C program that consists of a general algorithm:

        state= 0; get next input character
        while (not end of input) {
           depending on current state and input character
              match: /* input expected */
                 calculate new state; get next input character
              accept: /* current pattern completely matched */
                 perform action corresponding to pattern; state= 0
              error: /* input unexpected */
                 reset input; report error; state= 0
        }

and a decision table specific to the DFSA:

	a	b	c	d	e	other
0	match(1)
1		match(2)	match(2)
2				match(2)	match(3)
3	accept	accept	accept	accept	match(3)	accept

This table is indexed by the current state and input character, and used by the algorithm to decide which of the alternative actions to choose, and the new state after a match (the number in brackets in the table above). A blank indicates an error.

FLEX makes its decision table visible if we use the -T flag, but in a very verbose format. The DFSA it actually generates for this example has more states, but it does the same thing.

Parsers - Deterministic Push Down Automata (PDA)

The important difference between lexers, like those generated by LEX, and parsers, like those generated by YACC or JAVACC, is that the grammar rules for parsers can refer to each other - i.e. parsers have a limited memory, whereas lexers essentially have none. To provide for this, the PDAs used to implement parsers are basically DFSAs with a stack.

There are two important classes of parsers, known as top-down parsers and bottom-up parsers, and we are going to look at both in a bit more detail. They are important because they provide a good trade-off between speed (they read the input exactly once, from left-to-right) and power (they can deal with most computer languages, but are confused by some grammars). Other kinds of parsers can handle any grammar but take around O$(n^3)$ to process their input.

Either kind can be table-driven (e.g. LL(n) and LR(n)), and allow an action to be attached to each grammar rule, to be obeyed when the corresponding rule is completely recognised, similarly to LEX.

Top-Down Parsers

Here, the stack of the PDA is used to hold what we are expecting to see in the input. Assuming the input is correct, we repeatedly match the top-of-stack to the next input symbol and then discard them, or else replace the top-of-stack by an expansion from the grammar rules.

  initialise stack to be the start symbol followed by end-of-input
  repeat
    if top-of-stack == next input
      match -- pop stack, get next input symbol
    else if top-of-stack is non-terminal and lookahead (e.g. next input) is as expected
      expand -- pop stack (= LHS of grammar rule)
         and push expansion for it (= RHS of grammar rule) in reverse order
    else
      error -- expected (top-of-stack) but saw (next input)
  until stack empty or end-of-input

e.g. recognising a , b , c using:

list : id tail
     ;
tail :
     | ',' id tail
     ;

stack      next input   rest of input    action     ($ represents end-of-input)

$ list         a        , b , c $        expand list to id tail
$ tail id      a        , b , c $        match id a
$ tail         ,          b , c $        expand tail to ',' id tail
$ tail id ,    ,          b , c $        match ,
$ tail id      b            , c $        match id b
$ tail         ,              c $        expand tail to ',' id tail
$ tail id ,    ,              c $        match ,
$ tail id      c                $        match id c
$ tail         $                         expand tail to (nothing)
$              $                         accept

Typical top-down parsers are recursive-descent (e.g. JAVACC) and LL(n) parsers, which use n symbols of lookahead i.e. they make their decisions n symbols after the start of the sub-string of symbols that will match the next grammar rule. The grammars usable by top-down parsers normally have some restrictions:

Using the grammar list : id | id ',' list ; an LL(1) parser would get stuck when it tried to expand list on the stack with a next input of id - as both rules for list start with id, it wouldn't know which to pick without more lookahead. I factorised the grammar used above, to take out the common part of the two rules, and leave the remainder in tail. (We will look at this in more detail in $\S$6.2.)

Using the left-recursive grammar list : id | list ',' id ; an LL(n) parser could go into an infinite loop, expanding list on top of the stack to list ',' id, which would leave list on top of the stack, which would expand to ...

Bottom-Up Parsers

Here, the stack of the PDA is used to hold what we have already seen in the input. Assuming the input is correct, we repeatedly shift input symbols onto the stack until what we have matches a grammar rule, and then we reduce the grammar rule to its left-hand-side.

  initialise stack (to end-of-input marker)
  repeat
    if complete grammar rule on stack and lookahead (e.g. next input) is as expected
      reduce -- pop grammar rule and push LHS
    else if lookahead (e.g. next input) is as expected
      shift -- push next input, get next input symbol
    else
      error
  until stack==start symbol and at end-of-input

e.g. recognising a , b , c using:

list : id
     | list ',' id
     ;

stack      next input   rest of input    action

$              a        , b , c	$        shift id a
$ id           ,          b , c	$        reduce id to list
$ list         ,          b , c	$        shift ,
$ list ,       b            , c	$        shift id b
$ list , id    ,              c	$        reduce list ',' id to list
$ list         ,              c	$        shift ,
$ list ,       c               	$        shift id c
$ list , id    $                         reduce list ',' id to list
$ list         $                         accept

e.g. recognising a , b , c using:

list : id
     | id ',' list
     ;

stack          next input   rest of input    action

$                  a        , b , c $        shift id a
$ id               ,          b , c $        shift ,
$ id ,             b            , c $        shift id b
$ id , id          ,              c $        shift ,
$ id , id ,        c                $        shift id c
$ id , id , id     $                         reduce id to list
$ id , id , list   $                         reduce id ',' list to list
$ id , list        $                         reduce id ',' list to list
$ list             $                         accept

Typical bottom-up parsers are LR(n) parsers (e.g. YACC is LR(1)), which use n symbols of lookahead i.e. they make their decision n symbols after the end of the sub-string of symbols that will match the next grammar rule.

The stack actually holds an encoding of each symbol (the state) rather than the symbol itself. This encoding tells the parser anything it needs to know about the stack contents, so it only needs to look at the top item of stack rather than scan the whole stack to make a decision.
e.g. look back at list : id | list ',' id ; when the top of stack is an id and the next input is a , - we make different reductions depending upon the contents of the rest of the stack, which we actually do by having two different encodings (i.e. two different states) for id on the stack (telling us whether it was preceded by a , or not).

Top-Down parsers are simpler, so they are easier to understand, but harder to use, as they have difficulty coping with grammars that bottom-up parsers have no problem with. Right-recursive grammar rules cause bottom-up parsers to use more stack, but allow them to delay some decision making. (We will look at this in more detail in $\S$6)

A more detailed look at YACC parsers

Like LEX, YACC creates a C program that consists of a general parser algorithm (similar to that given in $\S$5.2.2) and a decision table specific to the grammar. For YACC, the parser algorithm is LR(1), and the decision table is created using the LALR(1) algorithm.

Just as with LEX, the decision table is indexed by the current state (initially set to 0) and the current input, and includes the value of the next state. However, during a reduction, the next state is found using the state on top of the stack after the RHS has been popped, and the LHS symbol that the RHS is being reduced to. We pop and push the states, rather than the symbols - as mentioned in $\S$5.2.2, the states encode the symbols plus any necessary extra information.

Although a simple stack of states is sufficient for the parsing algorithm, YACC's stack really consists of (state, value) pairs, where the value is set and used in the actions ($$, $1 etc.).

YACC allows us to use the -v flag to see its decision table in the file y.output
(for each state, the _ in the first line(s) tell us where we are in recognising the grammar, and the last line(s) are the transitions to other states. ``.'' means any (other) input symbol. $end means end of input)

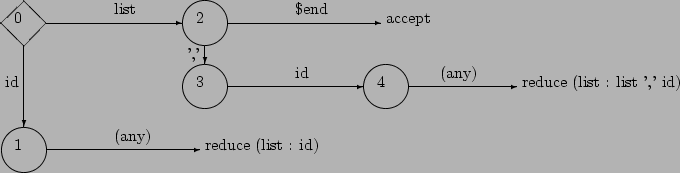
e.g. here is the (reformatted) y.output and corresponding decision table for list : id | list ',' id ;

state 0 $accept : _list $end
        id shift 1      . error        list goto 2
state 1 list : id_  (1)
        . reduce 1
state 2 $accept : list_$end
        list : list_, id
        $end accept      , shift 3     . error
state 3 list : list ,_id
        id shift 4       . error
state 4 list : list , id_  (2)
        . reduce 2

state	terminal symbols			non-terminals
	id	','	$end	list
0	shift 1			goto 2
1	reduce (list : id)
2		shift 3	accept
3	shift 4
4	reduce (list : list ',' id)

(non-terminal columns give the new state after a reduction)

(As mentioned in $\S$5.2.2, id is encoded by two different states - state 4 means it follows a , - state 1 that it doesn't.)

the corresponding PDA:

and some example parses: $[$stack+current state input symbol+rest of input ($=end of input)

$[$0 id$

$\rightarrow$

$[$01 $

$\Rightarrow$

$[$02 $

$\rightarrow$

accept

$[$0 id,id$

$\rightarrow$

$[$01 ,id$

$\Rightarrow$

$[$02 ,id$

$\rightarrow$

$[$023 id$

$\rightarrow$

$[$0234 $

$\Rightarrow$

$[$02 $

$\rightarrow$

accept

$\rightarrow$ = shift, $\Rightarrow$ = reduction

Each reduction pops the RHS to reveal a state which, with the LHS symbol, is used to decide the next state
(For this simple grammar always 0, list, and 2 respectively).

Epilogue

Most computer languages can mostly be processed by LR(1) parsers like YACC. This is partly because the ability of humans to understand a piece of text is similar to that of YACC, and partly because significantly more complex languages tend to be disproportionately harder and slower to translate, and so are rarely used. However, humans are smarter than computers, and translators have to be able to cope with worst cases, so it can sometimes be necessary to cheat slightly to be able to completely recognise a language.

Exercises

• Put some grammars through YACC -v and construct the corresponding PDAs from the y.output files.

• The simple translation of regular expressions to FSAs outlined above in $\S$5.1 usually creates a non-deterministic automaton (NFSA), which then has to be converted to a DFSA. e.g. consider:

    while|if   /* keyword */
    [a-z]+     /* identifier */
  

  Create an NFSA for these regular expressions, and then convert it to an equivalent DFSA that distinguishes between keywords and identifiers.

Readings

Capon & Jinks: chs. 6.4, 8.1, 8.4, 8.5
Aho, Sethi & Ullman: chs. 3.6-3.8, 4.5, 4.7
Johnson: $\S$4
Levine, Mason & Brown: p. 197