| name things | name : things ; |
| %% | |
| ...{name}... | ... name ... |
| LEX (may not recurse) | YACC (may recurse) |
| name : thing1 |
name : thing1 ; |
| name : thing2 ; |
name : and ;)
[ ]
? with LEX)
..
| (thing)+ | name : thing |
|
| or | name : thing |
|
| LEX | YACC |
| (thing)* | name : |
|
| or | name : |
|
| LEX | YACC |
|
We will use two different grammars, one right recursive:(Assume that we can recognise and convertexp : id | id '+' exp ;
and one left recursive:exp : id | exp '+' id ;
to recognisea + b + cas a expression.
a and b and c to identifiers somehow - they
are only used here to make the form of the parse trees clear.)
With both grammars, the form that expression nodes of the parse tree can
take is limited - either a single identifier or else a + with an
identifier on one (specified) side and an expression on the other
(i.e. another node). Therefore we have one node for each identifier. Of the
three expression nodes this implies, one will be just an identifier, and the
other two will also contain the two +s and subexpressions.
Example parse tree and equivalent fully-bracketed expression for
left-recursive and right-recursive grammars:
|
Therefore right recursive grammars should be used for right associative operators, and left recursive grammars for left associative operators.
e.g. part of a Pascal declaration:
decl : idlist ':' typeid ;
idlist : id | idlist ',' id ;
Each id recognised in idlist should be declared to be of type
typeid. e.g. for a , b : real we want to declare a and
b to each be real:
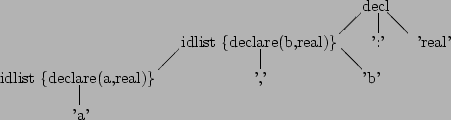
decl : idlist ':' typeid {$1 = $3;}
;
idlist : id {declare ($1, $$);}
| idlist ',' id {declare ($1, $$); $3 = $$;}
;
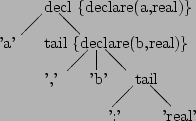
However, it is always possible to rewrite the grammar so that YACC can perform the calculations, although it may not always be easy or obvious. For example, the (left-recursive) grammar used above is really something like:
decl : id ( ',' id )* ':' typeid ;
and can be rewritten as (right-recursive):
decl : id tail {declare ($1, $2);}
;
tail : ',' id tail {$$ = $3; declare ($2, $3);}
| ':' typeid {$$ = $2;}
;
to give the following parse tree:
The example calculators given in ![]() 3 give different precedence
to the operators
3 give different precedence
to the operators +, -, *, /, ( and
) by using a separate grammar rule for each precedence level.
We can use left recursion for left associative operators and right recursion
for right associative operators (![]() 4.2). For
non-associative operators, we just do not use recursion at all
e.g.
4.2). For
non-associative operators, we just do not use recursion at all
e.g. a == b == c is legal in C but not in Pascal (which also uses
= instead of ==) so we could use this grammar rule for Pascal:
condition : exp '=' exp ;
The problem with these methods is that they tend to complicate the grammar
and constrain language design. YACC has an alternative mechanism that
decouples the declarations of precedence and associativity from the grammar,
using %left, %right and %nonassoc. e.g.:
%nonassoc '=' |
%left '+' '-' | increasing
%left '*' '/' |
%right '!' | precedence (i.e. not)
%right '^' v (i.e. exponentiation)
%%
exp : exp '+' exp | exp '-' exp | exp '*' exp | exp '/' exp
| number | '(' exp ')' | exp '^' exp | exp '=' exp | '!' exp
;
YACC can also give different precedences to overloaded operators; e.g. if - is used both for negation and for subtraction and we want to give them different precedences (and negation the same precedence as for not):
| '-' exp %prec '!'
To allow for any sort of associativity, we have had to use grammar rules in
the example that contain both left and right recursion - if it were not for
the %left etc., this grammar would be hopelessly ambiguous and so unusable.
(Disambiguation uses precedence first, then associativity, as expected.) The
converse of this is, that you must be careful how you use these facilities,
as they can conceal unexpected ambiguities in the grammar.
(![]() 6 will explore the problems of ambiguous grammars.)
6 will explore the problems of ambiguous grammars.)
As it stands, parsers generated by YACC halt at the first grammar error. This is not very informative to users, as there may be more errors to be found, so how can we improve error handling?
idlist : id
| idlist , id
| idlist id {yyerror ("missing ,");}
;
statement : variable ':=' expression
| . . .
| error
;
suggests where error recovery takes place. YACC also has actions
yyerrorok, yyclearin, YYACCEPT and YYERROR
to assist in this process.
Most modern parser-generators attempt, more or less successfully, to do both these levels of error recovery automatically, so all we have to write is the correct grammar. (Another reason to use a parser-generator, rather than write parsers by hand.)
A tool like YACC can cope with most combinations of precedence, associativity, number of operands and fix in expressions. It can even cope with most forms of overloading. However, YACC would have great difficulty in coping with an overloaded operator that had different precedence, associativity, number of operands or fix depending on its operands. Probably because most humans would also find this hard to cope with, I know of no such language.
Language designers can essentially ignore the difficulty of implementation of expressions and concentrate on usability, as the average user and the average compiler writer would probably agree about features they liked.
a AND (B OR Abcd_99 AND NOT (FRED OR TRUE))
\%left etc. You will need to merge and modify the rules for
exp, term and factor.
{, }, , and
; symbols. Is the error reported correctly, and is it located
accurately? Are there any subsequent spurious error messages? How
complicated a grammatical error can it cope with sensibly?
Louden: chs. 4.2, 4.4, 4.5
Capon & Jinks: chs. 6, 8.1, 8.4, 8.5, 8.6
Aho, Sethi & Ullman: chs. 2.2, 4.1, 4.3, 4.9, 5.1
Johnson
Levine, Mason & Brown: chs. 3, 7, 9