The previous section described an approach to partitioning
canonical loop nests, as introduced in Definition 1.
In this section we re-consider loop nests having the general form
shown in Figure 2, but without the restrictions
associated with Definition 1, except that
![]() (i.e., the loop nest is not empty). Then, applying
index set splitting, the original loop nest can be
transformed into multiple adjacent loop nests each of which
satisfies the requirements for partitioning set by Theorem
2 or it is rectangular.
(i.e., the loop nest is not empty). Then, applying
index set splitting, the original loop nest can be
transformed into multiple adjacent loop nests each of which
satisfies the requirements for partitioning set by Theorem
2 or it is rectangular.
Consider the loop nest shown in Figure 2;
the first step consists of finding the values of ![]() which satisfy
the inequalities
which satisfy
the inequalities
![]() If no such values exist, then the loop with index
If no such values exist, then the loop with index ![]() is never
executed. If there are such values, given by
is never
executed. If there are such values, given by
![]() ,
the loop with index
,
the loop with index ![]() is always executed; therefore, this loop is canonical
with respect to the outer loop, and no index
set splitting is required. Conversely, if there is a subset of the values of
is always executed; therefore, this loop is canonical
with respect to the outer loop, and no index
set splitting is required. Conversely, if there is a subset of the values of
![]() which satisfies both inequalities, say
which satisfies both inequalities, say
![]() , where
, where ![]() , then the outer
loop must be split into two consecutive loops, the first of which corresponds
to the values given by
, then the outer
loop must be split into two consecutive loops, the first of which corresponds
to the values given by
![]() , while the second corresponds
to
, while the second corresponds
to
![]() ; for the former values, the loop with
index
; for the former values, the loop with
index ![]() is canonical with respect to the outer loop, while, for the
latter, it is never executed.
is canonical with respect to the outer loop, while, for the
latter, it is never executed.
If, as a result of the previous step, there are some values of ![]() for which
the two outermost loops are canonical, the next step consists of finding
the values of
for which
the two outermost loops are canonical, the next step consists of finding
the values of ![]() which make the three outermost loops canonical;
these values must satisfy the system of inequalities
which make the three outermost loops canonical;
these values must satisfy the system of inequalities
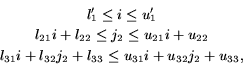
The same procedure is repeated for each loop, successively, until there
are no remaining loops or else a given system of, say ![]() ,
,
![]() ,
inequalities has no solutions (this would imply that the loop with
index
,
inequalities has no solutions (this would imply that the loop with
index ![]() is never executed for these values of
is never executed for these values of
![]() that render the
that render the ![]() outermost loops canonical). Note that, in
the case where the original loop nest contains more than one
consecutive loops at some level,
the same procedure should be applied for each loop separately.
outermost loops canonical). Note that, in
the case where the original loop nest contains more than one
consecutive loops at some level,
the same procedure should be applied for each loop separately.
Example 2Consider the loop nest shown in Figure 4.a. Since
there are two consecutive loop nests in the body of the I loop,
the procedure described above must be applied separately for each
of them.
For the first loop nest, the J loop is canonical with respect
to the outer loop; the K loop is canonical (with
respect to the I, J loops) when
2*I-J ![]() 1000
1000
![]() J
J ![]() 2*I-1000.
Thus, the J loop must be split into two consecutive loops
depending on which values of J render the K loop canonical;
the bounds of the first loop will be 1 and MAX(1,2*I-1000)-1,
and of the second loop MAX(1,2*I-1000) and I. Since
the body of the J loop does not contain statements other than
the K loop, no statements are executed in the case when
1
2*I-1000.
Thus, the J loop must be split into two consecutive loops
depending on which values of J render the K loop canonical;
the bounds of the first loop will be 1 and MAX(1,2*I-1000)-1,
and of the second loop MAX(1,2*I-1000) and I. Since
the body of the J loop does not contain statements other than
the K loop, no statements are executed in the case when
1 ![]() J
J ![]() MAX(1,2*I-1000)-1; hence, the
corresponding loop can be eliminated.
MAX(1,2*I-1000)-1; hence, the
corresponding loop can be eliminated.
For the second loop nest, the J loop is canonical with
respect to the outer loop when 2*I-500 ![]() 1000
1000
![]() I
I ![]() 750; the index of the I
loop is split accordingly. Furthermore, the K loop
is canonical when
I+J
750; the index of the I
loop is split accordingly. Furthermore, the K loop
is canonical when
I+J ![]() 1000
1000
![]() J
J ![]() 1000-I.
The code resulting after applying the appropriate transformations is
shown in Figure 4.b. Evaluating
MAX(1,2*I-1000), by replacing it with appropriate conditionals
which are then removed using index set splitting
(see Section 3.2),
results in the code shown in Figure 4.c
(note that MIN(1000,1000-I) is always equal to
1000-I since I takes only positive values). Finally,
partitioning I for each loop nest
as in Section 3.2,
and grouping the partitions according to (7) for
1000-I.
The code resulting after applying the appropriate transformations is
shown in Figure 4.b. Evaluating
MAX(1,2*I-1000), by replacing it with appropriate conditionals
which are then removed using index set splitting
(see Section 3.2),
results in the code shown in Figure 4.c
(note that MIN(1000,1000-I) is always equal to
1000-I since I takes only positive values). Finally,
partitioning I for each loop nest
as in Section 3.2,
and grouping the partitions according to (7) for ![]() ,
the partitioned code can lead to perfect load balance
when using 5 processors, and, in general, a comparatively low value of
load imbalance [15].
,
the partitioned code can lead to perfect load balance
when using 5 processors, and, in general, a comparatively low value of
load imbalance [15].![]()