The partitioning schemes described in Section 3.1
result in perfect load balance, or a small value of load imbalance,
when each iteration of the parallel loop performs the same amount of work.
A simple example where this is not the case
is that of a triangular loop nest; assuming that such a loop
having the index of the outer loop, ![]() , taking values from
, taking values from ![]() to
to
![]() , and the index of the inner loop taking values from
, and the index of the inner loop taking values from ![]() to
to ![]() ,
is mapped onto
,
is mapped onto ![]() processors, then, for
processors, then, for ![]() ,
the relative load imbalance has a lower bound of
,
the relative load imbalance has a lower bound of ![]() .
It is apparent that the partitioning schemes described so far are not
sufficient to minimise load imbalance; nevertheless, using these
as a basis, more appropriate schemes can be devised.
.
It is apparent that the partitioning schemes described so far are not
sufficient to minimise load imbalance; nevertheless, using these
as a basis, more appropriate schemes can be devised.
In the remainder of this paper we examine loop nests of depth ![]() having the
general form shown in Figure 2. It is assumed
that the sets of statements labelled statements.1,
statements.2,
having the
general form shown in Figure 2. It is assumed
that the sets of statements labelled statements.1,
statements.2, ![]() , statements.2m-1 do not include
statements whose execution depends
on the value of the index of a surrounding loop; hence,
the workload corresponding to each set
of statements remains the same for any iteration
of the outer loop. This, however, does not exclude the
possibility that, in any of the above-mentioned sets
of statements, DO
, statements.2m-1 do not include
statements whose execution depends
on the value of the index of a surrounding loop; hence,
the workload corresponding to each set
of statements remains the same for any iteration
of the outer loop. This, however, does not exclude the
possibility that, in any of the above-mentioned sets
of statements, DO ![]() ENDDO loops which perform the same number of
iterations regardless of the value of I, may exist.
Thus, literally, the depth of a loop nest may be higher than
ENDDO loops which perform the same number of
iterations regardless of the value of I, may exist.
Thus, literally, the depth of a loop nest may be higher than ![]() ; however,
in this and subsequent discussion, only those loops having bounds
dependent on the index of the outermost loop (directly or indirectly)
are considered; any remaining loops do not affect the strategy followed
and they are omitted.
; however,
in this and subsequent discussion, only those loops having bounds
dependent on the index of the outermost loop (directly or indirectly)
are considered; any remaining loops do not affect the strategy followed
and they are omitted.
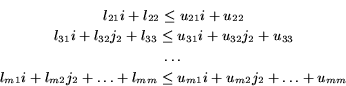
Based on Definition 1, the next theorem is proved [15]:
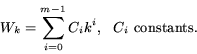
In order to illustrate Theorem 1 with an example, consider
again a triangular loop nest having the index of the outer loop, ![]() ,
taking values from
,
taking values from ![]() to
to ![]() , and the index of the inner loop taking
values from
, and the index of the inner loop taking
values from ![]() to
to ![]() ; then, assuming that
; then, assuming that ![]() is partitioned into
is partitioned into
![]() equal partitions, the
equal partitions, the ![]() -th partition,
-th partition, ![]() , exhibits
a workload equal to
, exhibits
a workload equal to ![]() , for
, for ![]() constants. This
property leads to the following [15]:
constants. This
property leads to the following [15]:
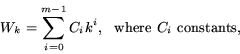
Theorems 1 and 2 can be summarised as follows:
In order to illustrate the results of Theorems 1 and 2, we consider the following example:
|
Example 1Consider the loop nest shown in Figure 3.a. Assuming that
N ![]() , then the inequalities -2
, then the inequalities -2 ![]() 3*I-1
and J+I
3*I-1
and J+I ![]() 5*I+2 always hold, while, for each inequality,
the coefficients
of I are non-zero; hence, the requirements of Definition 1
are satisfied and the loop nest is canonical for
5*I+2 always hold, while, for each inequality,
the coefficients
of I are non-zero; hence, the requirements of Definition 1
are satisfied and the loop nest is canonical for ![]() . Thus, based on
Theorems 1 and 2, and assuming that the
number of iterations of the outer loop, N, is a multiple of
. Thus, based on
Theorems 1 and 2, and assuming that the
number of iterations of the outer loop, N, is a multiple of ![]() ,
where
,
where ![]() is the number of processors,
partitioning the loop nest according to (7) leads to
perfect load balance; the partitioned loop nest is shown in
Figure 3.b.
is the number of processors,
partitioning the loop nest according to (7) leads to
perfect load balance; the partitioned loop nest is shown in
Figure 3.b.![]()
|
In the general case, where the number of iterations of the outer
loop, ![]() , is not a multiple of
, is not a multiple of ![]() , the partitioning
technique suggested by Theorem 2 can be applied,
provided that the outer loop is partitioned according to one
of the partitioning schemes described in Section 3.1. In this
case, a small value of load imbalance is expected.
, the partitioning
technique suggested by Theorem 2 can be applied,
provided that the outer loop is partitioned according to one
of the partitioning schemes described in Section 3.1. In this
case, a small value of load imbalance is expected.
Theorems 1 and 2 also apply to loop nests where there are more than one inner loops at the same level (i.e., loops which are surrounded only by the same outer loops) whose bounds depend on the index of a surrounding loop; the necessary proviso is that, for any loop in the nest, the lower bound is always less than or equal to the upper bound.