Ignoring the baggage that needs to be wrapped around a program e.g. in C:
int main (int argc, char*[] argv){ ... ;return 0;}
the minimal program in assembler is one instruction, in C or Java is one
statement,
etc.
What happens if we need to write a bigger program? In imperative and OO
paradigms (assembler, c, java), we can write several instructions or
statements one after the other.
However, we need to write programs that do more than just obey a simple
sequence of instructions, by using
assembler: un/conditional jumps, jsr/rts (bl/mov pc,r14), ...
c: loops (for, while, do), choices (if, if-else, switch), functions calls and
recursion
etc.
It looks like a programming language needs some sort of repetition, some sort of choice, and some sort of function call. Is this sufficient? (e.g. do we also need labels and go-tos?) Is this all necessary? (e.g. do we really need recursion?)
If we can do anything that computer hardware can do, then with sufficient ingenuity we can do anything that can be done with computers. Therefore, whatever hardware (i.e. assembly language) can do must be sufficient. However, assembly languages usually contain unconditional jumps, so maybe all programming languages need labels and go-tos?
``Bitter experience has shown that using labels and gotos to allow jumps to be made from any point of a program to any other point is a bad idea; it disperses logically related parts of the program, it obscures the flow of control so that we cannot decide which routes through the code are actually possible, and it encourages jumps into the middle of otherwise working constructions, violating their preconditions and generating untraceable bugs.'' [C.H.Lindsey]
In fact, even assembly language is more complex than we really need - if we can write a simulator for a computer, we can still do anything (even if very slowly). All we need for a simple simulator is: a single conditional loop (while not halted, obey the next instruction or micro-instruction step or whatever) containing a multi-way choice (switch/if-then-else-if...) which selects the operation to perform, and lots of variables representing the registers (including PC) and memory.
[If the computer we are simulating has complex operand forms, we may be able to save a lot of code by using several switch statements rather than one, or by using functions, but we can still write it all in one big switch statement if we are patient enough.]
This was first pointed out by Böhm and Jacopini, although not quite in this way. They actually showed how to take any imperative program and rewrite it to only use repetition and choice, and we will look at this in more detail later.
The sufficiency argument above also points towards the answer about necessity - we need one conditional loop mechanism and one multi-way choice mechanism in a programming language, and nothing more!
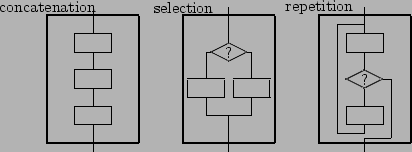
This is the foundation of structured programming, as proposed by Dijkstra -
you can write any program using (as many instances as you like of)
a single concatenation mechanism (;),
a single multi-way choice mechanism (e.g. if-then-else), and
a single conditional loop mechanism (e.g. recursion or while),
and arbitrary nesting of these (begin-end or { } blocks).

Anything else, including function calls (assuming you use a while loop rather
than recursion), is window dressing, allbeit highly important window dressing
if you want to write programs bigger than around a hundred lines.
(Dijkstra certainly expected programmers to use functions!)
[Dijkstra's repetition construct, which involves a test in the middle of the loop, is not often directly implemented in programming languages. However, special cases of it are common: a version with the first box missing so the test is at the start is found in most languages, and a version with the last box missing so the test is at the end is often found as well.]
LEX has repetition and choice, but no variables. YACC has the same facilities plus "functions". They are not able to do everything that a normal programming language can do, but this allows them to do their specialised task much more efficiently than would otherwise be possible (O(n)). YACC is more powerful than LEX, but more complicated and (linearly) slower.
e.g. LEX can't accurately recognise nested brackets - the best it can
do is something like "("+")"+ so the brackets don't have to match. It
has no variables to e.g. count the number of brackets and to check that they
match exactly. It is, of course, possible to do cleverer things in the
associated C action, but this is using the facilities of C, not of
LEX - as far as LEX is concerned, the string matched the
pattern, even if the C action subsequently spots an error.
e.g. YACC can match nested brackets
e.g. s : '(' ')' | '(' s ')' ;
because it can refer (in this example, recursively) to one grammar rule while
in the middle of another (rather than simply using tail/right recursion or
head/left recursion as a form of repetition) - essentially "remembering where
it is up to" so it can come back and finish matching this pair of brackets
later.
e.g. because YACC doesn't have variables to count with, even though it can match brackets, it can't deal with a string of "("s followed by the same number of "@"s followed by the same number of ")"s.
e.g. YACC can't deal with palindromes (strings that are their own
mirror images e.g. abba or abacaba) - you can write a YACC-like
grammar for palindromes, e.g.
p : 'a' | 'b' | 'a' 'a' | 'b' 'b' | 'a' p 'a' | 'b' p 'b' ;
but YACC finds lots of shift-reduce conflicts. Variables would
e.g. allow it to save the input until it has counted how many characters there
are, find the middle, and work outwards.
Another way of looking at this is that LEX and YACC have a very small state (just one internal value) and therefore can test it very quickly, but can't count past some small number (depending on the particular grammar) which will be too small to count the number of characters in a large enough string.
| level | grammar | machine | notation | recogniser | speed |
| 0 | UG | TM | infinite software | ||
| 1 | CSG | FTM | real software | compiler | |
| 2 | CFG | PDA | BNF | (prolog) | O( |
| LALR(1) | YACC | O(n) | |||
| 3 | RG | FSA | RE | LEX | O(n) |
A compiler is an ordinary program written in an ordinary programming language. However, parts of a compiler can be written using much more efficient systems (LEX and YACC). We try to maximise the parts of a compiler written using LEX and YACC, but some things (dealing with context i.e. declarations) are just too difficult for them.
Because of this, the part of the compiler that recognises the input is almost
always split into the same three distinct components:
The lexical analyser, the most efficient component, that deals with everything
that can be described by regular expressions, and is usually written using
LEX or something similar. Loosely, it combines characters into words.
The syntactic analyser, the next most efficient component, that deals with
everything left that can be described by BNF, and is usually written using
YACC or something similar. Loosely, it combines words into sentences.
The semantic analyser, the least efficient component, that deals with
everything that the previous components cannot handle, and is usually written
using an ordinary programming language. Loosely, it checks the meaning of the
sentences.
a;
while (b) {c; d;}
e;
if (f) g; else h;
i;
Start by replacing all control constructs with labels and gotos: (this step is similar to what you will see in CS2042, except that it is still written in C rather than being reduced to assembly code.)
a;
s1: if (!b) goto s3;
c; d; goto s1;
s3: e;
if (!f) goto s5;
g; goto s6;
s5: h;
s6: i;
Next, split the program up into linear sequences of code (each line in the example below) that always begin with a label and finish with a goto (i.e. we can't just fall through an if into the next piece of code, we have to put in "else goto next line"):
s0: a; goto s1; s1: if (b) goto s2; else goto s3; s2: c; d; goto s1; s3: e; if (f) goto s4; else goto s5; s4: g; goto s6; s5: h; goto s6: s6: i;
Finally, replace the labels and gotos by a switch inside a while, and use a variable, s, to hold the state number:
s= 0;
while (s >= 0) switch (s) {
case 0: a; s=1; break;
case 1: if (b) s=2; else s=3; break;
case 2: c; d; s=1; break;
case 3: e; if (f) s=4; else s=5; break;
case 4: g; s=6; break;
case 5: h; s=6; break;
case 6: i; s=-1; break;
}
This can also be used to obfuscate a program, particularly if you also shuffle and renumber the cases.
a; b(); c;
. . .
void b(void) {x;}
becomes:
case 0: a;
r=1; s=99; break; /* call b */
case 1: c; . . .
. . .
case 99: x; /* function b */
s=r; break; /* return */
I am simply using another variable, r, to hold the state number to return to after the call. This is obviously limited and we will generalise it in the next example.
a; d= b(i, j); c;
. . .
float b (int m, int n) {float p; p= m+n; return p;}
becomes:
union {float b;
int main;
. . . /* one entry for the result for each function */
} result;
struct stacktype {
struct stacktype * previous;
int r;
union {struct {int argc; char**argv; int i, j;} main;
struct {int m, n; float p;} b;
. . . /* one entry for the parameters and variables of each function */
} frame;
};
struct stacktype * sp= NULL, * t;
struct stacktype * push (struct stacktype * previous, int r)
/* malloc a new struct stacktype and return a pointer to it,
after initialising the "previous" and "r" fields */
struct stacktype * pop (struct stacktype * old_frame)
/* free "old_frame" and return a copy of its "previous" field */
. . .
case 0: a;
t=push(sp, 1); t->frame.b.m=sp->frame.main.i; /* call b */
t->frame.b.n=sp->frame.main.j; sp=t; s=99; break;
case 1: d=result.b; c; . . .
. . .
case 99: sp->frame.b.p=sp->frame.b.m+sp->frame.b.n;
result.b=sp->frame.b.p; /* function b */
s=sp->r; sp=pop(sp); break; /* return */
The original implementation of Quicksort was in a language that did have functions but did not support recursion, and so the recursion had to be expanded out something like this (but I suspect Hoare used an array and indices rather than a list and pointers).
The previous section is not the whole truth: it is possible to write C programs that this scheme will not work for, but it does work for most straightforward C programs, is much easier to understand than the real answer, and - if you knew what went wrong - from here you could work out the real answer if you ever needed to.
If you take CS2042, you will get a look at the real answer (but in assembler rather than in c, so it is much simpler).
Dijkstra: Goto considered harmful
CACM V11 #3 pp.147-148 (March '68)
http://www.acm.org/classics/oct95/
or
http://doi.acm.org/10.1145/362929.362947
Dijkstra: Notes on structured programming pp17-19
in Dahl, Dijkstra & Hoare: Structured programming
Academic Press 1972
Böhm & Jacopini: Flow diagrams, Turing machines, and languages with only
two formation rules
CACM V9 #5 pp.336-371 (May '66)
http://doi.acm.org/10.1145/355592.365646