



Next: Abstract Data-Types, Modules, Classes
Up: CS2111: Design and Implementation
Previous: Composite Types
Contents
Subsections
Vectors and Arrays - Language design and implementation
The possible values for each index of each array are defined by the upper and
lower bounds, which in many languages can be any integer
or even any scalar (other than reals).
The same information may be expressed by the number of elements if the
language fixes the lower bound.
A sequence of e.g. words or bytes, depending on the element type.
May need extra information, depending on operations (see below).
We will model an array variable as a set of as many locations as the array
has elements, each mapped to a value according to the state. Then the
variable access array[index] just selects the correct location from the
array variable and proceeds as for a simple variable.
To simplify finding the location(s) for a particular element of an array, we
place the locations used for the array at a regular pattern of addresses, so
array[index] is at address
origin + index * stride,
where the origin is the starting address for the array and the
stride is the constant offset between the addresses of the locations of
successive elements of the array. (The origin is the address of
array[0]; if 0 is not a valid index then the origin is not an address
of an element of the array.)
For simple languages, a compiler can recalculate the stride from the element
type whenever necessary, so the only information needed to access an array
is its origin.
In many languages
we should check that each index falls in the permitted range i.e.
lower bound 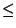 index
index 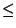 upper bound
The compiler needs to know what the bounds are e.g. from the declaration. If
the lower bound is fixed, and especially if it is zero, this is even simpler.
If the array is dynamic (see below) this is harder.
Most languages allow multi-dimensional arrays, either by having multiple
indices or by permitting the element type to itself be an array, although some
have a maximum allowed number of dimensions.
upper bound
The compiler needs to know what the bounds are e.g. from the declaration. If
the lower bound is fixed, and especially if it is zero, this is even simpler.
If the array is dynamic (see below) this is harder.
Most languages allow multi-dimensional arrays, either by having multiple
indices or by permitting the element type to itself be an array, although some
have a maximum allowed number of dimensions.
Many modern languages treat an array as a vector whose elements may be of
(almost) any type, including arrays. Thus, a 2-dimensional array is just a
vector of vectors. Some languages make this clear in declarations and/or
accesses, e.g. using a[i][j],
some languages hide this e.g. using a[i,j],
and some allow both forms,
although they may not treat them in exactly the same way.
Element access is similar to that for vectors, except that after each index
(except the last) is processed, the calculated address is just used as the
origin for the next index calculation; if we have processed all the indices
then this is the correct address.
The stride is calculated from the array declaration. Many languages leave
this to the implementor; the simplest method is to use the size of a vector
element, calculated from its type (which may itself be a vector). Some
languages insist that the strides are calculated in a specific way (usually
similar to this simple method) so that:
the user knows exactly how memory is used,
or
the bounds of one dimension can be dynamically varied at run-time, so this
dimension (either the first or the last for a multi-dimensional array) must
have the largest stride.
Algorithms for array accesses:
| |
access |
bchk |
stride(s) |
| 1-D |
O+I*S |
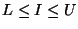 |
S=sizeof(element) |
| multi-D |
O+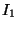 * *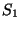 |
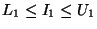 |
 = " = " |
| |
+ * *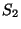 |
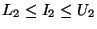 |
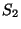 = " *( = " *(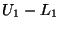 ) ) |
| |
. . . |
. . . |
. . . |
| |
+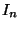 * *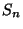 |
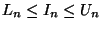 |
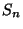 = " *( = " *(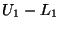 )* . . . *( )* . . . *(
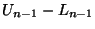 ) ) |
<>
(note: 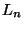 and
and 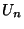 are not required to calculate S)
Some languages require the size of arrays to be known at compile-time
(static arrays),
usually by restricting bounds to literals, or to constants, or to constant
expressions.
are not required to calculate S)
Some languages require the size of arrays to be known at compile-time
(static arrays),
usually by restricting bounds to literals, or to constants, or to constant
expressions.
Some languages allow the size of arrays to be computed at run-time
(dynamic arrays),
so bounds can be any expressions - this can cause difficulties for the
implementor and so is controversial - some languages only permit this for one
dimension (either the first or the last) of a multi-dimensional array, and/or
only allow it for anonymous variables.
Some languages can query a vector (usually a parameter) to
find its upper and/or lower bounds,
or iterate over all elements of a vector.
The less that the compiler knows at compile-time, the more it has to calculate
and pass around at run-time. For example, if a language has both dynamic
arrays and bound checking, then the bounds (and strides) of arrays have to be
decided at run-time, when the array is created, and passed on if the array
is used as a parameter.
So, in a simple language a vector parameter passed by reference is just the
origin, but in a more complex language we need more information. This can be
either auxiliary vectors of pointers (Iliffe vectors - see exercises)
or of dimensional information (dope vectors). The latter is essentially
a list of triples of (lower bound, upper bound, stride), with one triple for
each dimension. (This is assuming a language where the lower bound is not
fixed - if it was we would only need a pair for each dimension.)
Implementation of operations on arrays:
| |
fixed |
variable |
|
| static |
1-D |
S L&U |
O |
| |
multi-D |
S L&U |
O |
| dynamic |
1-D |
S |
O L&U |
| |
multi-D |
- |
O S L&U |
| slice |
|
- |
O S L&U |
<>
(note: if no bound-checking is required, simply ignore L&U.)
Static arrays passed as parameters have to be treated like dynamic arrays
unless the bounds are fixed at compile time, e.g. by type-checking.
Some languages require implementations that calculate and keep this
information in a dope vector at run-time, as it allows the most generality for
e.g. array slicing or dynamic arrays.
Other languages, that constrain array declarations or operations, can have
implementations that fix some or all of these at compile time, and so
allow faster code.
- Some languages can copy or compare vectors.
- Some languages can only initialise vectors.
e.g.
int a[] = {1, 2, 3, 4, 5};
some languages allow e.g. {6=>3, 7..15=>4, others=>-1}
- Some languages support slicing - selecting a subset of the
array elements
e.g.
b is a [15 : 17] or a [ : 17] or a [15 : ]
In Pascal, arrays are defined to be built so that:
a: array [1..4, 1..7] of integer;
means exactly the same as:
a: array [1..4] of array [1..7] of integer;
and thus either a[i, j] or a[i][j] can be used interchangeably.
Therefore only the first dimension can be sliced, and only to select one
element (row or column): a[i].
If the language allows slicing, then any array may be a slice from a
higher-dimension array, so every array has to be treated as if it is dynamic
- the origin, bounds and strides can only be calculated once the slice has
happened, at run-time.
- When multiplication took longer than a memory access, a common
implementation of multi-dimensional arrays was to use Iliffe vectors
i.e. an array is a vector of pointers to vectors of pointers to... to vectors
holding the actual elements. e.g. a 2-D array of integers is a vector of
pointers to vectors of integers. During an access, the first index selects a
pointer from the initial array, and the second index selects an integer from
the vector pointed at.
This technique makes array slicing asymmetrical, as we can slice via the one
index but not via the others. As the vectors of values are independent, they
can in principle, have different sizes and bounds from each other.
In many languages it is possible for the user to explicitly write code to
use Iliffe vectors. Using C, declare and access a 2-dimensional array using
this technique. You will also need to ensure that the vectors of values
exist and initialise the vector of pointers. Try obtaining the space for the
values in two ways: using malloc, and using another local variable of
suitable size.
Louden: chs. 5.1, 5.2, 5.4, 5.5
Bal & Grune: chs. 2.2.1, 2.3, 2.3.1
Aho, Sethi & Ullman: ch. 7.1




Next: Abstract Data-Types, Modules, Classes
Up: CS2111: Design and Implementation
Previous: Composite Types
Contents
Pete Jinks
1999-09-30