CS646: DL Reasoning

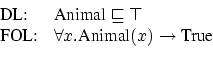
NOTE: This document is also available at http://www.cs.man.ac.uk/~horrocks/Teaching/cs646/Labs/dlreasoning/.

1 OWL Abstract Syntax

As well as the rather verbose RDF/XML syntax, OWL also has a ``human readable'' syntax which is (rather oddly) called the abstract syntax. The abstract syntax corresponds very closely to the ontology structure presented by Protégé, i.e., Class and Property ``definition'' axioms, plus axioms to capture additional information such as disjointness and other background facts not represented in the ``definitions''. A complete specification of the abstract syntax can be found at http://www.w3.org/TR/owl-semantics/syntax.html; some examples of the abstract syntax and equivalent RDF/XML syntax can be found at http://www.w3.org/TR/owl-semantics/examples.html#B.1.


Consider the following small ontology written in OWL abstract syntax:


Class(Animal partial)
Class(Plant partial)
DisjointClasses(Animal Plant)
ObjectProperty(eats domain(Animal))
Class(Herbivore complete super(restriction(eats allValuesFrom(Plant))))
Class(Carnivore complete super(restriction(eats allValuesFrom(Animal))))
Class(CarnivorousPlant complete super(Plant) super(Carnivore))


The first axiom, i.e., Class(Animal partial), can be translated into an equivalent DL axiom and into equivalent FOL as follows:

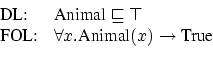
\begin{displaymath}\begin{array}{ll} \mbox{DL:} & \mbox{Animal} \sqsubseteq \to... ...forall x .\mbox{Animal}(x) \rightarrow \mbox{True} \end{array}\end{displaymath}

Write down DL and FOL equivalents of each of the other axioms in the ontology.

2 DL Reasoning

  1. Enter the above ontology into Protégé, and use the reasoner to compute the class hierarchy.

  2. Explain why Plant is a sub-class of both Herbivore and Carnivore.

  3. This does not seem to be correct. Explain how you would improve the ontology in order to fix this problem.

  4. Did your improvement reveal any other problem with the ontology? If so, how would you repair the problem?

3 DL Semantics

Consider the following small Knowledge Base (ontology) $ \mathcal{K}$, where $ \mathcal{K}$ consists of the following set of axioms:

Person $\displaystyle \sqsubseteq$ $\displaystyle \top$  
Man $\displaystyle \sqsubseteq$ Person  
Woman $\displaystyle \equiv$ Person$\displaystyle \sqcap \neg$Man  
Parent $\displaystyle \equiv$ Person$\displaystyle \sqcap \some{\mbox{hasChild}}{\mbox{Person}}$  
Father $\displaystyle \equiv$ Man$\displaystyle \sqcap$   Parent  
Mother $\displaystyle \equiv$ Woman$\displaystyle \sqcap$   Parent  
TwoChildFather $\displaystyle \equiv$ Father$\displaystyle \sqcap \atleast{2}{\mbox{hasChild}} \sqcap \atmost{2}{\mbox{hasChild}}$  
HappyFather $\displaystyle \equiv$ Father$\displaystyle \sqcap \some{\mbox{hasChild}}{\mbox{Man}} \sqcap \some{\mbox{hasChild}}{\mbox{Woman}}$  
TiredParent $\displaystyle \equiv$ Parent$\displaystyle \sqcap \atleast{5}{\mbox{hasChild}}$  
hasChild $\displaystyle \sqsubseteq$ hasDescendant  
hasDescendant$\displaystyle ^+$ $\displaystyle \sqsubseteq$ hasDescendant  
hasAncestor $\displaystyle \sqsubseteq$ hasDescendant$\displaystyle ^-$  
John $\displaystyle :$ Man  
Mary $\displaystyle :$ Woman  
$\displaystyle \langle$John$\displaystyle ,$Mary$\displaystyle \rangle$ $\displaystyle :$ hasChild  

and the interpretation $ \I = (\deltai,\cdot\ifunc)$ of $ \mathcal{K}$, where
$\displaystyle \deltai$ $\displaystyle =$ $\displaystyle \{a, b, c, d, e, f, g, h\}$  
John$\displaystyle \ifunc$ $\displaystyle =$ $\displaystyle a$  
Mary$\displaystyle \ifunc$ $\displaystyle =$ $\displaystyle b$  
Person$\displaystyle \ifunc$ $\displaystyle =$ $\displaystyle \{a, b, d, f, g, h\}$  
Man$\displaystyle \ifunc$ $\displaystyle =$ $\displaystyle \{a, g, h\}$  
hasChild$\displaystyle \ifunc$ $\displaystyle =$ $\displaystyle \{(a,b), (a,h), (b,d), (g,a), (g,f) \}.$  


  1. Extend to give extensions to the other concepts (classes) in $ \mathcal{K}$ and roles (properties) in the Knowledge Base (ontology), i.e., complete the following:
    Woman$\displaystyle \ifunc$ $\displaystyle =$    
    Parent$\displaystyle \ifunc$ $\displaystyle =$    
    Father$\displaystyle \ifunc$ $\displaystyle =$    
    Mother$\displaystyle \ifunc$ $\displaystyle =$    
    TwoChildFather$\displaystyle \ifunc$ $\displaystyle =$    
    HappyFather$\displaystyle \ifunc$ $\displaystyle =$    
    TiredParent$\displaystyle \ifunc$ $\displaystyle =$    
    hasDescendant$\displaystyle \ifunc$ $\displaystyle =$    
    hasAncestor$\displaystyle \ifunc$ $\displaystyle =$    

  2. Is the extension of any of the concepts empty? If so, does this mean that these concepts are unsatisfiable? Explain your answer.
  3. Is the extension of HappyFather empty? If not, does this mean that HappyFather is satisfiable w.r.t. $ \mathcal{K}$? Explain your answer.
  4. Is the extension of TwoChildFather equal to the extension of HappyFather? If so, does this meant that the two concepts are equivalent w.r.t. $ \mathcal{K}$ (i.e., that $ \mathcal{K} \models$   TwoChildFather$ \equiv$   HappyFather)? Explain your answer.
  5. Is the extension of John in the extension of HappyFather? Does this meant that John is and instance of HappyFather w.r.t. $ \mathcal{K}$ (i.e., $ \mathcal{K} \models$   John$ :$HappyFather)?

4 Ontology Examples

Load the People and Pets ontology (http://www.cs.man.ac.uk/~horrocks/Teaching/cs646/Labs/PeopleAndPets.owl) into Protégé. Work through the examples in the Reasoning with OWL lecture notes (http://www.cs.man.ac.uk/~horrocks/Teaching/cs646/Slides/why.ppt), checking the various inferences using Protégé and making sure you understand why the inferences are being drawn.

この文書について...

CS646: DL Reasoning

この文書はLaTeX2HTML 翻訳プログラム Version 2002-2-1 (1.70)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds,
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

を日本語化したもの( 2002-2-1 (1.70) JA patch-2.0 版)

Copyright © 1998, 1999, Kenshi Muto, Debian Project.
Copyright © 2001, 2002, Shige TAKENO, Niigata Inst.Tech.

を用いて生成されました。

コマンド行は以下の通りでした。:
latex2html -numbered_footnotes -split 0 dlreasoning.

翻訳は Ian Horrocks によって 平成16年11月19日 に実行されました。