Magic Pi – The Magic of NumbersToby HowardThis article first appeared in PC Advisor magazine, May 1998. WHILE WE SEEM TO COPE with the idiosyncrasies of PCs, not to mention the peculiarities of the Internet, many people find mathematics not only baffling, but also downright frightening. It's true that in 1910, Bertrand Russell and Alfred North Whitehead took over 360 pages of densely packed argument in their huge book Principia Mathematica to prove that 1 + 1 = 2. But you don't need a PhD in Advanced Maths to have fun with numbers. In this article we'll look at a tiny sample of the wonders of numbers, and I hope you'll join me in enjoying some of their strangeness. It's amazing that all computing is done just by juggling 0's and 1's – nothing and something. Just as computers couldn't exist without numbers, so the latest developments in many branches of mathematics – like proving computer programs to be correct – would be impossible without computer assistance. Patterns and Palindromes"A man, a plan, a canal – Panama!" That's an example of a palindrome – a word or phrase that reads the same forwards as backwards. Numbers can be palindromic too, like 10,662,526,601 (it's 22013). Or take 262,808, add 4 to get 262,812, and multiply the two numbers together. The result is the extraordinary palindrome 69069096096. Here's a simple recipe for finding a palindromic number. Start with any number, reverse its digits, and then add the two numbers. Keep repeating the process and eventually a palindromic number should emerge. We can try it with 87, for example: 87 + 78 = 165; 165 + 561 = 726; 726 + 627 = 1353; 1353 + 3531 = 4884. We found a palindrome in 4 steps. Or again with, say, 159, which only takes two steps: 159 + 951 = 1110; 1110 + 0111 = 1221. The number of steps is unpredictable: try it with 89 and you'll need 24 – to get to 8,813,200,023,188! It's been found that all numbers less than 10,000 will produce a palindrome in this way with one bizarre exception – the number 196. Although it's been taken through hundreds of thousands of reverse-and-add steps, leading to giant 80,000-digit numbers, no palindrome has yet been found. What's so special about 196 – in all other respects a seemingly ordinary number? And do all numbers eventually produce a palindrome using the reverse-and-add method? Nobody knows the answers. Isn't it strange that something so simple should remain a mystery? Read on. Pi in the skyTake a circle. Measure its circumference, then measure its diameter. Now divide the circumference by the diameter. The answer you get is the same for any circle you can ever draw, and it's a truly universal result. A three-headed lizard-man from the Crab Nebula, assuming he could draw circles, would find exactly the same number. It's pi, and it's fascinated people for millennia. pi is an extraordinary number. It's "irrational", meaning it cannot be written as the ratio of two whole numbers. It's also "transcendental", because it cannot be the solution to any algebraic equation. 22/7 is a useful simple approximation to pi, evaluating to 3.142857 to six decimal places, but pi's true value to six decimal places is 3.141593. In fact, the decimal expansion of pi continues without limit, and people have devised all kinds of methods for working out more and more digits (see the box the first 1,000). The current record stands at almost six and a half billion digits, and you can actually get them from ftp://www.cc.u-tokyo.ac.jp. Isn't the Internet wonderful?
As well as encapsulating the "circle-ness" of circles, pi crops up in all kinds of unexpected places. For example: imagine you randomly threw a needle onto a flat board ruled with parallel straight lines. What is the probability that the needle will land across one of the lines? The answer is directly proportional to 1/pi. And not a circle in sight! We can also conjure pi out of the whole numbers, like this: pi2/6 = 1/12 + 1/22 + 1/32 + 1/42 + 1/52 + . . . Or we can do it with just the odd numbers: pi/4 = 1 – 1/3 + 1/5 – 1/7 + 1/9 – 1/11 + . . . Or their squares: pi2/8 = 1/12 + 1/32 + 1/52 + 1/72 + 1/92 + . . . Or with evens and odds combined: pi = 2/1 * 2/3 * 4/3 * 4/5 * 6/5 * 6/7 * . . . It's rather mysterious that a number we associate so closely with circles can also arise out of simple counting. But that's nothing when you consider the "famous five" equation, which draws together five of the most fundamental numbers in mathematics: 0, 1, pi , e (the base of natural logarithms) and, most spookily of all, i, the square root of –1: ei * pi + 1 = 0 Logarithms, circles, complex numbers, addition, nothing (0), something (1) – all in one simple equation! Something very surprising about pi was discovered recently. It's always been assumed that if you want to know the digit at some position in the expansion of pi , you have to work out all the other digits leading up to that point. But a formula was discovered in 1995 that lets you extract a single digit from pi without bothering to compute any of the rest. Many mathematicians were utterly astonished that such a formula could exist at all, because it went against centuries of conventional wisdom. The maths involved is too lengthy to describe here, but you can find all the details, and a C program to try for yourself, at www.mathsoft.com/asolve/plouffe/plouffe.html. (There is a catch, by the way – the method only works if pi is written in base 16. The race is currently on to find a formula which works with our normal base-10 notation.) So pi arises out of all the integers, and all the integers occur in pi . It's natural to wonder if there's any significance to the digits of pi . Might there be, as Carl Sagan suggested in his novel Contact, a message from the Creator hidden deep within its digits? Alas no: despite some surprises like finding 999999 at position 762, and 314159 at position 176,451, statistical tests have shown the digits in pi are completely random. In fact, since the expansion of pi is infinite, all possible sequences of numbers will eventually turn up. This may sound like a far-out idea, but you can test it for yourself by searching the first 50 million digits of pi for any sequence of digits you like at www.aros.net/~angio/pi_stuff/piquery.html. Or why not try searching pi for your birth date, at www.facade.com/Fun/amiinpi/. Meanwhile, if you want to try to remember just the first 15 digits of pi , try this mnemonic: "How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics!" pi is weird and wonderful indeed, and two great places to start exploring its oddities further are www.users.globalnet.co.uk/~nickjh/Pi.htm and www.yahoo.com/Science/Mathematics/Numbers/Specific_Numbers/Pi/. Primes, Codes and GIMPSPrime numbers have become big news in recent years, because as well as being the source of more mathematical conundrums than you can shake a stick at, they also hold the key to the best method of cryptography ever invented. A prime number is an integer that can only be divided by two numbers without leaving a remainder. Those two numbers are itself, and 1. For example, 6 is not a prime number – you can divide it exactly by 2 and 3. They're called the factors of 6. Nor is 143 prime – it can be divided exactly by its factors 11 and 13. But numbers such as 11, 23, 137, 1009, 27827, 597823, 244497 – 1, cannot be divided up in this way. They're primes, and the box lists all such numbers less than 1000 (to see a few more, you can download the first 100,000 from www.utm.edu/research/primes/lists/small/100000.txt.).
How many primes are there altogether? Euclid proved the answer over 2,000 years ago: there are infinitely many. The problem is finding them – as you can see from the box, they seem to appear rather chaotically.
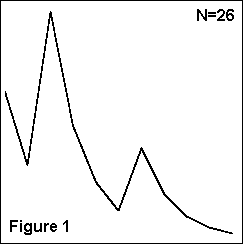
As of late 1997, the largest known prime number is 22976221 – 1, although by the time you read this article, a larger number may have been discovered. [It has. 23021377 – 1 was discovered in early 1998 by Ronald Clarkson, a student at California State University.] 2 2976221 – 1 is a monstrous number with 900,000 digits, which using this typeface would take up over half of PC Advisor. Remembering I get paid by the page, I tried this on with the Editor, but he wouldn't buy it. In fact 22976221 – 1 is a special kind of prime, known as a Mersenne prime. Mersenne numbers all have the form 2n – 1, and only some of them are prime. It was on August 24th, 1997 that Gordon Spence of Glasgow completed the proof that 22976221 – 1 was indeed prime. He used a humble 100 MHz Pentium PC. Gordon is one of over 2,000 enthusiasts world-wide in the GIMPS program – the Great Internet Mersenne Prime Search. The idea is to spread the search for primes across many independent searchers, so they can collectively cover a huge amount of ground simultaneously. It's a kind of virtual parallel supercomputer – spread across the Internet. For details of how to join in, and to download the free software and databases, see www.mersenne.org. You might even get into the record books! You may be wondering if there's a point to all this. There is. Prime numbers are of supreme practical importance because of their use in "public-key cryptography", currently the most secure code we have. The idea is to choose two very large primes – say P and Q – and to multiply them together, to get a third number, say R. R is then used as a key in the coding system to encrypt a message. But there's a twist: to decrypt the message, P and Q are needed. It's a secure system because, given any particular large number R, it's incredibly hard to reverse engineer it to find its two prime factors P and Q. In fact for large numbers it would require centuries of computation. It's a fair bet that deep in the offices of Intelligence Agencies around the world, mathematicians are toiling to find out how to factor huge numbers. If they succeed, all our most advanced codes will be rendered useless overnight. Simple questions, hard answersOne of the most intriguing – and inexplicable – aspects of mathematics is that some problems are extremely simple to describe, but turn out to be incredibly difficult to solve – if not impossible. Here area few examples, to give you a flavour of this weird situation. Fermat's Last Theorem is perhaps the most famous mathematical problems ever. Since it first appeared in about 1637, it resisted proof for over 350 years. Yet it's so simple to describe. Look at this equation: z2 = x2 + y2 Many readers will recognise this as Pythagoras's famous theorem about right-angled triangles: "the square on the hypotenuse is equal to the sum of the squares on the other two sides". Obviously, there are many numbers that satisfy this equation. In fact there are an infinite number of solutions – just like there are an infinite number of right-angled triangles. But what about this variation: z3 = x3 + y3 It looks very much like the Pythagoras formula, except we're now cubing the numbers. What made Fermat famous was that he stated there were no three whole numbers x, y and z that will make this equation work. In fact he went much further, saying that for any equation of the form: zN = xN + yN if N was bigger than 2, there are no whole positive numbers x, y, and z that will satisfy the equation. And how did Fermat justify this amazingly sweeping statement? He wrote as follows, as an annotation in a book he was reading: "I have discovered a truly marvellous proof of this fact, which, unfortunately, this margin is too small to contain." It was to take mathematicians until 1995 to find a watertight proof of Fermat's bold claim. The proof, by the Princeton University mathematician Andrew Wiles, involves some extremely advanced and difficult concepts, and all sorts of mathematical theories that hadn't even been invented in Fermat's time. It's very hard stuff, and it's thought that only a few hundred of today's mathematicians can actually follow Wiles's proof in detail. So did Fermat really have a proof up his sleeve? It seems doubtful. Here's another problem that non-mathematicians can easily understand, yet this one has turned out to be a stinker to prove. Whether it's true or not, nobody knows. It's called the Goldbach Conjecture, and it states that every even number bigger that 2 is the sum of two primes. Some examples: 12 = 5 + 7, 124 = 53 + 71, 1248 = 617 + 631, and so on. You can try it with any number you like at www.vex.net/~buff/cgi/goldbach.cgi. Goldbach's Conjecture has been confirmed by computer tests to be true up to 1014 – but no one has been able to prove that it works for every possible even number. Some arithmetical questions are so simple it's bewildering that they remain unsolved. Take "hailstone numbers", for example. Start with any positive integer – call it N. If N is even, replace N with N/2; if N is odd, replace N with 3N + 1. Repeat these steps until you get N=1. For example, if we choose 12 as our starting number, we get the sequence 12, 6, 3, 10, 5, 16, 8, 4, 2, 1. You might like to try this out with a few different starting numbers. You should find that no matter what number you choose, it will eventually reach 1, although the number of steps required will vary. Stefan Wolfrum has written a program for Windows 95 that lets you interactively experiment with hailstone numbers and see graphs of their behaviour. I used it to create Figure 1, which shows the behaviour of N = 26: it takes 10 steps to get back to 1 (shown on the horizontal axis), increasing and decreasing in size in the process (shown on the vertical axis).
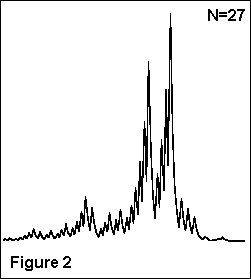
Figure 2 shows what happens when N = 27. We now have 111 steps of chaos, rising as high as 9,232 before reaching 1. You can download Stefan's program from titan.informatik.uni-bonn.de/~wolfrum/.
Incredibly, no one has yet been able to prove that all numbers will eventually reach 1. Nor is there any proper understanding of the chaotic behaviour of this simple procedure: the number of steps required for a given number to reach 1 varies wildly, as Figures 1 and 2 show. And finally . . .Even maths has its limits. G÷del's Incompleteness Theorem, only discovered in 1931, says that within any formal system with its own rules and conventions, there are some facts within that system that are true, but which cannot be proved to be true using the rules of the system. The problem is finding out which facts fall into that category. It's an unsettling, rather Kafkaesque, situation. But now my space is up, and I find I haven't even mentioned knots, googols, fractals, perfect numbers, the different kinds of infinity, tessellations, symmetries, groups – all topics in the domain of the recreational mathematician. If any of the ideas in this article have got you thinking, it's easy to follow them up. And if you have a PC on your desk, you have the most powerful tool ever invented for the exploration of these ideas – except, of course, for your imagination.
Toby Howard teaches at the University of Manchester. |