Proof Methods for Multi-Agent Systems
- A Case for Support
RENATE SCHMIDT
Department of Computer Science,
University of Manchester
EMAIL:
schmidt@cs.man.ac.uk
URL: http://www.cs.man.ac.uk/~schmidt/
MICHAEL FISHER, CLARE DIXON
Department of Computer Science,
University of Liverpool
EMAIL:
M.Fisher@csc.liv.ac.uk,
C.Dixon@csc.liv.ac.uk
URL: http://www.csc.liv.ac.uk/~michael/,
http://www.csc.liv.ac.uk/~clare/
This project will be undertaken by the Department of Computing and
Mathematics at the Manchester Metropolitan University, under the
management of Renate Schmidt, Michael Fisher and Clare Dixon.
is a Senior Research Lecturer in the
Department of Computing and Mathematics at Manchester Metropolitan
University.
She is an expert on automated proof methods,
resolution decision procedures, non-classical logics and relational
algebras.
Her research has led to several contributions on
- efficient automated reasoning for expressive modal logics and description
logics [22,27,29,28,30,32,43,44],
- translating logics and simulating proof procedures in first-order
logic [32,39,44],
- resolution-based proof techniques and decision procedures for
solvable first-order
classes [30,31,43],
and
- relation algebraic structures and their exploitation in AI
systems [4,5,45].
From 1991 to 1997 she was employed as a research associate
at the Max Planck Institute of Computer Science in Saarbrücken.
She was awarded an MSc degree in the Department of Mathematics at the
University of Cape Town, in 1991, for her work relating well-known
algebraic structures to knowledge representation.
Her investigations
were conducted partly while being a guest at the Automated Reasoning
Project of the Australian National University in Canberra in the summer
of 1989/90, made possible by a vacation scholarship.
In 1997 she obtained the degree of Dr. Ing. from
the Technische Fakultät of the Universität des Saarlandes in
Saarbrücken, for research into translation based modal theorem
proving [42].
Her thesis studies optimisations of the functional translation method of
propositional modal logics into first-order logic as well as optimisations
of proof procedures on such translations.
Currently, Dr. Schmidt is a grant holder of
- an EPSRC PhD grant ``Path-Based Reasoning about Guarded Formulae'' (GR/M36700) to
begin in September 1999.
In the past she has
worked on a number of projects, including
``Transformation of Logical Systems'' (DFG), ``Construction of Non-Classical Logics'' (German-French
PROCOPE Programme), ``Techniques for Inference in Communicating Systems'' (DFG). She has been the recipient of a travel grant from the British Council/NWO
for collaborative work with Utrecht University.
is a Professor in the
Department of Computing and Mathematics at Manchester Metropolitan
University. He is well-known for his work on temporal reasoning,
programming languages, multi-agent systems and concurrent
theorem-proving, having developed
- a resolution-based proof method for a range of temporal
logics [10,16,17],
- a significant multi-agent programming language, based upon
executable logic [15],
- a formal framework for the specification and verification of
multi-agent systems [20], and
- a novel framework for concurrent and agent-based
theorem-proving [14,19].
He has over twelve years experience in the specification, verification
and implementation of concurrent and distributed systems, covering
research into temporal specifications [20],
verification via both proof and model-checking
[9], and implementation using executable
logics [13], particularly applied to the area of
multi-agent systems [12,18].
Professor Fisher has edited volumes entitled ``Executable Modal and
Temporal Logics'' (Springer-Verlag, 1995) and ``The Imperative
Future'' (Research Studies Press, 1996), and was a guest editor for
the Journal of Symbolic Computation (November/December, 1996). He is
principal investigator on the current EPSRC research grants ``Proof
Methods for Temporal Logics of Knowledge and Belief'' (GR/K57282) and
``Developing Clausal Resolution for the Temporal 2#2-Calculus''
(GR/L87491), and was a grantholder on the ``Parallel Temporal
Theorem-Proving'' project (GR/J48979), which was completed in December
1996.
He is the organiser of a number of workshops on executable logics (in
1993, 1995 and 1997), multi-agent systems (in 1996, 1997 and 1998),
automated reasoning (in 1997) and temporal reasoning (in 1999). He is
programme chair for many of these events and is also a programme
committee member for a variety of international conferences and
workshops.
is a Senior Research Lecturer in the Department of Computing
and Mathematics at Manchester Metropolitan University. She is well known
for her work on proof methods for modal and temporal logics in particular
- resolution methods for linear-time temporal logics
[7],
- efficient proof search in temporal logics [8],
- resolution and tableau based proofs for temporal logics of knowledge
[10,51].
Dr. Dixon obtained her PhD in 1995 from the University of Manchester
for research into temporal theorem proving. Her work focussed, in particular,
on the development of
algorithms to implement a temporal resolution based theorem prover
[7,17], proof
of their correctness, and strategies to guide the proof
search. Since then Dr. Dixon has worked as a Research Associate on the EPSRC project
``Parallel Temporal Theorem Proving'' (GR/J48979) investigating how the
temporal resolution method
may be parallelised and as a Research Fellow at the Manchester Metropolitan
University on the EPSRC project ``Proof Methods
for Temporal Logics of Knowledge and Belief'' (GR/K57282). This ongoing project
is investigating the development and evaluation of proof methods for logics
with both a temporal
and a modal dimension, suitable for analysing distributed and multi-agent
systems. Proof methods for the basic logics have been developed based on
tableau [51] and resolution
[10].
Currently Dr. Dixon is a grant holder of
- an EPSRC PhD grant ``Resolution Based Theorem Proving for Temporal Logics of Knowledge
and Belief with Interactions'' (GR/M44859).
Dr. Dixon is a member of the program committee for the international
workshop series on temporal representation and reasoning (TIME)
and is one of the program co-chairs for the 1999 event.
In summary, our methods have strong theoretical and practical
implications for many
areas of computer science where logics similar to those which
form the basis of most agent based systems are used.
For instance:
- Propositional normal modal logics with one or more
modalities.
- Extended multi-modal logics
such as propositional dynamic logic,
dynamic modal logic,
information logics, and
Humberstone's bimodal logic of inaccessible worlds.
- Many of the logics
in the hierarchy of description logics prominent in the field of knowledge
representation.
- Tarski's relational calculus, including for instance allegories
which have practical significance in work on hardware and circuit
design, or the Lambek calculus.
- Propositional temporal logics and combinations with knowledge and belief
logics.
- Maslov's class K, an expressive solvable first-order class into which
many expressive modal and relational logics, as well as first order
logic restricted to two variables (FO3#3) can be
embedded.
Thus, the applicants' expertise on (this variety of) non-classical logics,
expressive solvable first-order classes, proof methods for temporal
and modal logics, concurrent agent-based theorem proving, and empirical
testing, ensure
that this is an ideal team to lead the proposed project.
The Logic and Computations Research Group to which the three applicants
belong forms a node of
the AgentLink network, an ESPRIT-funded Network of Excellence
for agent-based computing.
(AgentLink coordinates the organisation
for research and development activities in the area of agent-based
computer systems funded by the European Commission.)
Background
Agent-Based Systems is widely recognised as an area of rapidly increasing
importance [33,50].
Agents provide a key abstraction within modern development of AI systems
and software.
Although there exist powerful theoretical models of agency
[41,47],
the techniques for solving the reasoning problem within these theories
have not been investigated sufficiently and proof systems have not
been applied in practical agent systems.
This project will apply the know-how and tools established and
produced in previous
work to develop proof methods for the expressive combinations of
diverse logics used in agent theories, and apply these to
particular examples from agent-based systems.
A multi-agent system is a collection of semi-autonomous processes known as
`agents' which live in dynamic and unpredictable environments.
Agents continuously interact which each other and the environment
and need to reason about their own and other agent's attitudes.
A typical example which is relevant to
accident analysis [34] is as follows.
Given that the pilot agent knows that at least one of the two engines is
working, and believes that the left engine is on fire (i.e.
4#4),
it follows that
the pilot agent would shut down the left engine next (i.e.
5#5).
Other characteristic applications include cooperative information
gathering (where a group of agents cooperate to access
distributed information sources in order to resolve a
user-generated query), other web applications such as information retrieval
and user profiling, as well as in industrial process control (e.g. air
traffic control, factory process control), business
process and workflow modelling, space shuttle fault diagnosis, and
electronic commerce [33,50].
A number of theoretical frameworks specifying agent-based systems
have been proposed, for example, the BDI model
being developed at AAII in
Australia [40,41], the
powerful KARO framework being developed at
Utrecht University [47],
temporal logics of knowledge and
belief [11,25,26],
and also more recent developments in modal description
logics [1,49].
These theories are being used for the specification and formalisation
of agent-based systems, yet the much needed techniques to analyse
and manipulate such specifications, utilising symbolic information
to determine appropriate behaviour, are only slowly beginning to
emerge [38].
For example, tableaux for multi-modal belief or knowledge logics
[25],
tableaux for multi-modal belief or knowledge logics with
linear-time temporal logic in [51], tableaux for belief-desire-intention
logics with either linear or branching-time temporal logics
in [40], and
resolution for knowledge logics with linear-time temporal logics
in [10].
The key problem in addressing the reasoning problem within multi-agent
systems is the inherent complexity of the agent scenarios.
The logics introduced in existing specification frameworks
are often first-order and tend to have a rich repertoire of modal
operators to model the range of the agents' mental attitudes and
the environmental states.
Typically, these include the following:
- Informational attitudes.
- Agents can reason about their own knowledge and belief
and about those of other agents.
In changing situations the knowledge of agents can change and agents
may need to revise their beliefs.
Notions of knowledge and belief are often formalised
in epistemic modal logics [25,36,46].
- Dynamic activity.
- Agents can perform actions, and agents need to have the
opportunity and ability to do so.
Propositional dynamic logic (PDL) has been used to specify
the results of actions and to define the concepts of opportunity
and ability [37,47].
Temporal logics are also useful for modeling complex dynamic environments,
where situations change over time as a result of actions
being performed.
Linear and branching time temporal logics have both been used to
capture the temporal aspects of agent-based
systems [26,40,41].
- Motivational attitudes.
- Fundamental motivational attitudes commonly used in agent theories
are intentions, wishes and goals.
Based on its knowledge of its goals and the practical possibilities an agent
may make certain commitments, which need to be stored and
maintained.
As soon as it no longer knows its commitments to be useful and
practically possible an agent is able to undo
commitments [6,47].
The specification of the mental and dynamic states usually
incorporates combinations of multi-modal logics, temporal
logics and first-order logic.
The degree to which combinations of these are useful and manageable
depends on the kind of interactions existing between the logics.
These vary in kind and complexity in different systems.
Some common and natural interactions include:
- Interaction between actions and attitudes.
On the one hand attitudes may change as actions are performed, while on
the other it is reasonable to assume, for example, that
an agent never forgets the effects of an action that it has anticipated
beforehand.
- Interaction between motivational attitudes.
Starting with an agent's wish, wishes induce goals which
do not yet hold, but are within the agent's practical possibility to
bring about (implementable wishes).
Wishes which are as yet unfulfilled but are implementable qualify then as its
goals.
- Interaction between knowledge and motivational attitudes.
This is the most complex form of interaction in agent-based systems
which is modelled in a multi-dimensional combination of logics endowed
with special model-transforming operations [47].
- Interaction between time and intentions.
Intention entails a form of commitment to intentions which need to be
maintained over time [24].
Although the basic properties of some of the individual logics are
well-understood, less is known about different interactions,
and very little work has been carried out on proof methods for such
complex logics.
Independent combinations of logics, or more precisely, combinations of
logics with propositional logic as their common part, inherit the
logical and model-theoretical properties of the individual
logics [48].
While logical properties, such as decidability and the finite model property,
transfer easily in these cases, properties specific to proof systems,
such as completeness, do not transfer easily.
That is to say, it may be that not all validities can be inferred in the
combined proof system, which is
essentially due to proof search strategies developed for the individual
logics interfering with each other when combined in one system.
Also, particular strategies which work well for propositional logic or
Horn logic are often not suitable for more expressive logics.
When the dynamic components (the different
modalities) of the logics interact, the situation is much more complicated.
Certain kinds of properties cause severe problems.
For example, `triangular' properties, which arise in agent theories, are
particularly hard to control in a proof system.
Whereas basic modal logics defined over transitive accessibility relations are decidable and
manageable (though not easily), in general, decidability is quickly lost
when considered in a more general logical context or when combined with
other logics, including modal
logics [23,35].
Even in very basic settings which are decidable, for example, a single
modal logic, special proof techniques are needed for predicates
with `triangular' properties, and with the exception of a few
(for example, transitivity or euclideanness) none have so far been developed.
As outlined in Part 1 we have developed sophisticated proof techniques
for a number of modal and temporal logics as well as expressive
first-order fragments into which certain combinations of modal logics
can already be embedded.
We are confident that considerable advances are now
possible in tackling more complex reasoning problems of agent-based
systems.
Hence, we believe that this project will provide an important step
towards the development of formal methods for agent-based systems and
the expansion of known results in the areas of agent modelling as well
as modal logic and automated reasoning.
The long term goal of our work is to provide practical proof systems
and automated reasoning tools for the development of multi-agent
systems.
We are interested in intelligent agent systems which present
particularly challenging problems.
Our work will focus on the reasoning problem for
complex combinations of expressive modal logics, temporal logics and
first-order logic as well as unconventional application-oriented
logics (e.g. with model-transforming operations) which form the basis
of common specification frameworks for modelling agent behaviour.
Powerful proof techniques are now available and provide viable
means for efficient and practical reasoning in a wide range of
non-classical logics and first-order classes.
We wish to study to what extent these new methods can be utilised
and enhanced for the development of feasible proof systems suitable to
meet the reasoning needs of agent-based systems.
Our principal objectives for this three year project are:
- The investigation of the computational properties of
interactions common in multi-agent systems: Which
interactions are decidable? Which undecidable interactions can be
approximated by something sufficiently expressive but decidable?
- The development, where possible, of terminating, automatic proof procedures
with special emphasis on simplification and redundancy elimination,
and where possible and feasible, the implementation of these inside
existing first-order theorem provers.
- The identification of general principles correlating particular
logics, clausal classes or their combinations, with particular techniques
for guiding search during the computation.
- The investigation to which extent sound and complete proof procedures of
single logics can be combined to form sound and complete proof
procedures for the comination of these logics.
Are there general compatability criteria for combining different proof methods?
For most of the investigation we will attempt to accommodate the
problem inside first-order logic and first-order resolution.
However, the formal framework
in which our study is situated is amenable to non-clausal (potentially
modal and temporal) resolution as well.
We adopt the resolution framework of Bachmair and
Ganzinger [2,3],
in which Robinson's resolution inference rule is enhanced by
ordering refinements which were originally developed to speed up
equational proof systems,
selection strategies, and
a general notion of redundancy elimination.
Our choice is motivated by the following considerations.
- The framework provides a generic and
application-independent platform, not restricted to clausal logic or
first-order logic [3].
- The available concepts of refinement and simplification are ideally
suited for the development of proof techniques,
tailor made for specific semantic theories or interactions.
Very few proof systems offer this level of
sophistication.
- Well-developed implementations of this framework are available.
- Other approaches, such as tableaux-based proof methods, can be seen to be
notational variants of particular instances of the
framework [30,32].
- By working with a first-order formulation which follows the semantic
definition of the logics of multi-agent systems, we avoid having to
address the problem of axiomatisability as the resolution calculus
immediately provides a sound and complete proof system.
In addition we will use SCAN [21], an indispensable
tool for computing first-order properties corresponding to non-standard
interactions between modal operators.
Naturally the work will build on
- the logical specifications and formal
methodologies developed in the different agent frameworks, including
the BDI model and the KARO framework,
- the model and proof theoretical foundations of various logics of knowledge and belief,
temporal logics and dynamic logics, and
- existing proof methods for these logics.
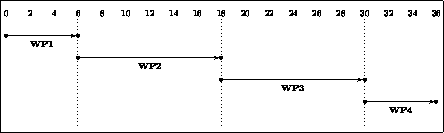
The research programme is broken down into four workpackages,
and each workpackage is further divided into tasks. For each
workpackage, we present an overview of the tasks, the
methodology to be utilised, and the deliverables to be produced.
Throughout the aim is to gain more knowledge about the computational
properties, ways of controlling and pruning search, and obtaining
decision procedures, where this is possible (i.e. main objectives 1 and 2 above).
Objectives 3 and 4 are the main concern in the last two workpackages.
The development of efficient proof methods for combinations of logics
with static interactions (on the proposional level), but
no dynamic interactions (between the modal operators).
(Month 1 to Month 6)
TASKS:
- 1.1
- Examination of different theoretical specification
frameworks modelling intelligent agents and investigation of
common combinations of logics with no or very limited interaction.
- 1.2
- Specification of a translation approach, different basic proof methods
and strategies for theorem proving tasks via first-order, modal and
temporal resolution.
- 1.3
- Collection of examples to be used for testing the ideas and techniques
developed in subsequent workpages.
- 1.4
- Identification of non-trivial interactions with respect to relevant logical
properties (such as decidability, non first-order definability), which are
to receive special attention in WP2 and WP3.
METHODOLOGY:
As there is not one single specification framework, we will begin by
examining the different existing frameworks for common combinations
of logics.
From on-going collaboration with
Utrecht University and previous work we have a some background of the
needs for the KARO framework and the BDI agent
architecture.
A range of different translation methods of modal logics into
first-order logic have been developed.
Each have advantages and disadvantages.
The optimised functional and semi-functional
translation methods have clear computational
advantages [29,42,44]
for standard modal logics, but their suitability for the required
combinations of logics needs to be investigated.
As mentioned before, even if there is no or very limited interaction
between the modalities this does not mean that search strategies
developed for individual logics are compatible when combined in one proof
procedure.
DELIVERABLES: Principles of efficient proof
for independent joins of the relevant logics.
(Report.)
TOTAL: 6 PERSON-MONTHS
The development of efficient proof methods, where possible decision
procedures, for combinations of modal logics
with non-trivial interactions identified in workpage WP1.
(Month 7 to Month 18)
TASKS:
- 2.1
- Interacting epistemic and dynamic
modalities.
- 2.2
- Interacting epistemic and temporal
modalities.
- 2.3
- Investigation of the combination first-order resolution and
inductive reasoning needed for combinations with
dynamic and temporal logics.
METHODOLOGY:
An example interaction property relating epistemic and dynamic
modalities is the principle of accordance:
6#6,
where 7#7 means agent 8#8 knows 9#9, and
10#10
means after executing action 11#11 property 9#9 is always true.
It says that an agent 8#8 never forgets the effects of an action
that he anticipates beforehand.
Similar principles connect epistemic modalities and temporal
modalities.
This kind of interaction is known to be dangerous and
decidability is quickly lost [25,26,35].
Even if the logics are only semi-decidable our aim is to enhance
performance by utilising existing notions of redundancy elimination
and developing new (e.g. semantic) simplification techniques for
avoiding unnecessary search.
The point of departure for Task 2.3 will be our previous work on temporal
resolution [10,16,17].
DELIVERABLES:
First-order characterisation, principles of efficient proof and
computational characterisation. (Report.)
TOTAL: 12 PERSON-MONTHS
The development of efficient proof methods, where possible decision
procedures, for combinations of first-order
and modal logics with non-trivial interactions.
(Month 19 to Month 30)
TASKS:
- 3.1
- Interacting epistemic and
motivational operations.
- 3.2
- Interacting epistemic, dynamic, temporal and
motivational operations.
- 3.3
- Extraction of general combination principles.
METHODOLOGY:
Foreseeably, these are the most difficult tasks and at this stage it
may only be possible to approximate the intended effects of commitment,
undoing, and maintenance.
We will want to find suitably expressive approximations/abstractions
which are sound (that is, logical consequences should be valid).
Already on the specification level these notions need to be modelled
outside well-behaved modal logics by a model-transforming operation
(mentioned in Section A).
Virtually nothing is known about this type of construction, except for
a definition of the semantics which attempts
to capture the intuition behind commitment and undoing.
Thus, it needs to be investigated whether it will be necessary to
develop a completely new proof method.
We envisage that our previous work on expressive solvable
classes [31] provides a broad enough basis for
attacking this problem.
This type of operation clearly complicates also the
interactions between the modal logics investigated in WP2, as now
predicates depend on additional arguments.
Even though the combinations of logics needed in multi-agent systems
may turn out to be undecidable, which is very likely, the aim of
Task 3.3 is to identify principles and strategies which provide fast
decision procedures for as many as possible of the decidable reducts.
DELIVERABLES:
Development of proof methods and refinements for the combination of first-order
fragments and various modal logics.
General principles of combining different proof methods. (Report.)
TOTAL: 12 PERSON-MONTHS
Application of the developed methods to some simple case studies
from the literature, evaluation and comparison of the different
methods and strategies, and the development of a prototypical
implementation as an extension of an existing first-order theorem prover.
(Month 31 to Month 36)
TASKS:
- 4.1
- Designing and implementing an input language
suitable for agent specifications, and translation to first-order logic.
- 4.2
- Implementing and testing of different proof strategies.
METHODOLOGY:
To gain more insight about the computational properties of the logics
investigated and the effects of different strategies in
practice, different refinements will be implemented and tested on
reasonably sized examples collected in WP1 and throughout the project.
Most likely we will extend the theorem prover SPASS for which we
have already implemented a prototypical front-end which automatically
translates modal and relational formulae into first-order logic.
DELIVERABLES:
Prototypical implementation.
(Report.)
TOTAL: 6 PERSON-MONTHS
Final report and prototype proof system.
DUE AFTER: 36 MONTHS
The management of the project will be carried out by the principal
investigators.
In order to ensure progress towards the goals of
the project frequent meetings will be held.
In addition, to annual reports on progress and potential problems, the
results emanating from this project will be widely disseminated through
conferences, journals and electronic forums.
Reasoning about agents in complex dynamic environments presents a major
challenge in AI research.
Such reasoning is crucial and pervasive to most agent applications.
In addition, this work provides a complex test case for
automated reasoning techniques, and very likely will require
new solutions, with significant implications for other areas
of computer science.
In the short term the principal beneficiary of this work will be the
research communities involved with agent-based systems, non-classical
logics, proof theory and automated reasoning.
However, we believe that, in the medium term, the techniques developed
will enhance our ability to formalise and reason about a wide range
of real world situations.
The results will be presented at recognised conferences (listed in
below)
and will be published in respected journals.
Among the most important journals through which our results may reach a
wider audience are the Journal of Automated Reasoning, the
Journal of Logic and Computation, the Journal of Applied
Non-Classical Logics, the Journal of Symbolic Logic, the
Journal of Symbolic Computation and
Artificial Intelligence.
A practical outcome of the project will be a prototype
automated proof system for intelligent agent systems,
which will be made publicly available by FTP or WWW.
Justification of Resources
We require funds to support one research associates for three
years. A research background in the theory, application and practical
aspects of modal and temporal logics is clearly essential for
investigation into this area. We are fortunate to know of an
excellent candidate, Ullrich Hustadt, who we hope we can attract to
support this work.
Ullrich Hustadt graduated with the German equivalent of a
Masters degree in Computer Science (Diplom) in 1991 from the
University of Dortmund. From 1991 to 1998 he was a Research Associate
at the Max Planck Institute of Computer Science in Saarbrücken.
Currently, he is a Research Fellow in the Department of Computing and
Mathematics at MMU working on the EPSRC funded project ``Proof Methods
for Temporal Logics of Knowledge and Belief'' (GR/K57282). He is
currently awaiting his viva for a PhD from the University of the
Saarland, Germany. His research centers around
resolution-based and tableaux-based decision procedures for decidable
fragments of first-order logic, including fragments resulting from the
relational, semi-functional and optimised functional
translation of decidable propositional modal
logics [22,28,30,31].
Moreover, his work is concerned with the design and
analysis, both theoretical and empirical, of modal theorem
provers [27,28,29].
His experience and background means that he is ideally placed to
contribute substantially to the proposed project.
Finally, we request 10% of a software technician's time and 10%
of a secretary's time at the Manchester Metropolitan University to
support the project.
One high performance PC, together with networking and printing
facilities, will be required for producing high-quality conference
and journal papers and for development work during the project.
A number of visits are planned between Utrecht University and the
Manchester Metropolitan University.
We also plan for visits to various academic and industrial sites within
the United Kingdom, including Queen Mary & Westfield
College, King's College, Imperial College London, the Universities of Birmingham,
Cambridge, Edinburgh, Essex, Glasgow, Leeds, Newcastle, Oxford, Ulster, Warwick,
and York.
Within Europe there are several centres where important related
research developments are underway, for example Amsterdam,
Saarbrücken (MPII, DFKI), Berlin (TU), Karlsruhe, Kaiserslautern,
Munich (TUM), Marseilles, Paris, Toulouse (IRIT), Grenoble (IMAG),
Moscow, Trento (IRST), Aarhus (BRICS), Stockholm (SICS), Warsaw, Oporto and Barcelona (IIA).
We wish to maintain contact and collaborate with such groups on
related problems and expect several, week long, visits to be made by
the participants over the lifetime of the project.
Finally, further funds will be required to visit and maintain contact
with major groups in AAII (Melbourne), ANU
(Canberra), Argonne (Illinois), NJIT (New Jersey), SUNY,
Toronto, Austin, Stanford, MIT, CMU, Syracuse and Japan.
Thus, we request funds to make visits to academic and industrial
research sites, and to attend conferences in such areas.
Relevant conferences include ATAL, CADE, IJCAI, AiML, JELIA, ICTL,
KR, FroCoS, FLoC, DISCO, ECAI, AAAI, LICS, TABLEAUX, TIME, HICSS, ISC,
TARK, DL, ILPS, ICLP, TPHOL, IFIP, MFCS, CSL, CAV, FME, POPL, PLILP,
EXTOL, ICMAS, SCAI, FAPR, AIMSA, together with workshops on agents,
automated reasoning, non-classical logics and knowledge representation.
- 1
-
F. Baader and H. J. Ohlbach.
A multi-dimensional terminological knowledge representation language.
J. Appl. Non-Classical Logics, 2:153-197, 1995.
- 2
-
L. Bachmair and H. Ganzinger.
Rewrite-based equational theorem proving with selection and
simplification.
J. Logic Computat., 4(3):217-247, 1994.
- 3
-
L. Bachmair and H. Ganzinger.
A theory of resolution.
To appear in Handbook of Automated Reasoning, 1997.
- 4
-
C. Brink, K. Britz, and R. A. Schmidt.
Peirce algebras.
Formal Aspects of Computing, 6(3):339-358, 1994.
- 5
-
C. Brink and R. A. Schmidt.
Subsumption computed algebraically.
Computers and Mathematics with Applications, 23(2-5):329-342,
1992.
- 6
-
P. R. Cohen and H. J. Levesque.
Intention is choice with commitment.
Artif. Intell., 42:213-261, 1990.
- 7
-
C. Dixon.
Search strategies for resolution in temporal logics.
In Proc. CADE-13, vol. 1104 of LNAI, pp. 672-687.
Springer, 1996.
- 8
-
C. Dixon.
Removing irrelevant information in temporal resolution proofs.
J. Experimental and Theoret. Artif. Intell., 11:95-121,
1999.
- 9
-
C. Dixon and M. Fisher.
Tableaux for Synchronous Systems of Knowledge and Time with
Interactions.
In Proc. SCAI'97. IOS Press, 1997.
- 10
-
C. Dixon, M. Fisher, and M. Wooldridge.
Resolution for temporal logics of knowledge.
J. Logic Computat., 8(3):345-372, 1998.
- 11
-
R. Fagin, J. Y. Halpern, Y. Moses, and M. Y. Vardi.
Reasoning About Knowledge.
MIT Press, 1995.
- 12
-
M. Fisher.
Representing and executing agent-based systems.
In Intelligent Agents. Springer, 1995.
- 13
-
M. Fisher.
An introduction to executable temporal logics.
Knowledge Engineering Review, 11(1):43-56, 1996.
- 14
-
M. Fisher.
An Open Approach to Concurrent Theorem-Proving.
In Parallel Processing for Artificial Intelligence, vol. 3.
Elsevier, 1997.
- 15
-
M. Fisher.
Implementing BDI-like systems by direct execution.
In Proc. IJCAI'97. Morgan-Kaufmann, 1997.
- 16
-
M. Fisher.
A normal form for temporal logics and its applications in
theorem-proving and execution.
J. Logic Computat., 7(4):429-456, 1997.
- 17
-
M. Fisher and C. Dixon.
Guiding clausal temporal resolution.
In Proc. ICTL. Kluwer, 1997.
To appear.
- 18
-
M. Fisher and M. Wooldridge.
A logical approach to the representation of societies of agents.
In Artificial Societies. UCL Press, 1995.
- 19
-
M. Fisher and M. Wooldridge.
Distributed problem solving as concurrent theorem-proving.
In Multi-Agent Rationality, vol. 1237 of LNAI.
Springer, 1997.
- 20
-
M. Fisher and M. Wooldridge.
On the formal specification and verification of multi-agent systems.
Intern. J. Cooperative Inform. Systems, 6(1), 1997.
- 21
-
D. M. Gabbay and H. J. Ohlbach.
Quantifier elimination in second-order predicate logic.
S. Afr. Computer J., 7:35-43, 1992.
- 22
-
H. Ganzinger, U. Hustadt, C. Meyer, and R. A. Schmidt.
A resolution-based decision procedure for extensions of K4.
To appear in Advances in Modal Logic, Vol. 2, CSLI Publ.,
1999.
- 23
-
H. Ganzinger, C. Meyer, and M. Veanes.
The two-variable guarded fragment with transitive relations.
To appear in Proc. LICS'99.
- 24
-
M. P. Georgeff and A. S. Rao.
The semantics of intention maintenance for rational agents.
In Proc. IJCAI'95, pp. 704-710. Morgan Kaufmann, 1995.
- 25
-
J. Y. Halpern and Y. Moses.
A guide to completeness and complexity for modal logics of knowledge
and belief.
Artif. Intell., 54:319-379, 1992.
- 26
-
J. Y. Halpern and M. Y. Vardi.
The complexity of reasoning about knowledge and time. I lower
bounds.
J. Computer and System Sci., 38:195-237, 1989.
- 27
-
U. Hustadt and R. A. Schmidt.
On evaluating decision procedures for modal logics.
In Proc. IJCAI'97, vol. 1, pp. 202-207. Morgan Kaufmann,
1997.
- 28
-
U. Hustadt and R. A. Schmidt.
Simplification and backjumping in modal tableau.
In Proc. TABLEAUX'98, vol. 1397 of LNCS, pp. 187-201. Springer, 1998.
- 29
-
U. Hustadt and R. A. Schmidt.
An empirical analysis of modal theorem provers.
To appear in J. Appl. Non-Classical Logics, 1999.
- 30
-
U. Hustadt and R. A. Schmidt.
Issues of decidability for description logics in the framework of
resolution.
In Proc. FTP'98, LNAI. Springer, 1999.
To appear.
- 31
-
U. Hustadt and R. A. Schmidt.
Maslov's class K revisited.
To appear in Proc. CADE-16, LNAI, Springer, 1999.
- 32
-
U. Hustadt and R. A. Schmidt.
On the relation of resolution and tableaux proof systems for
description logics.
To appear in Proc. IJCAI'99, Morgan Kaufmann, 1999.
- 33
-
N. R. Jennings and M. Wooldridge.
Applications of agent technology.
In Agent Technology: Foundations, Applications, and Markets.
Springer, 1998.
- 34
-
C. W. Johnson.
The formal analysis of human-computer interaction during accidents
investigations.
In People And Computers IX, pp. 285-300. Cambridge Univ. Press, 1994.
- 35
-
M. Kracht.
Highway to the danger zone.
J. Logic Computat., 5(1):93-109, 1995.
- 36
-
J.-J. C. Meyer and W. van der Hoek.
Epistemic Logic for AI and Computer Science.
Cambridge Univ. Press, 1995.
- 37
-
R. C. Moore.
Reasoning about knowledge and action.
In Proc. IJCAI'77, pp. 223-227. Morgan Kaufmann, 1977.
- 38
-
D. T. Ndumu and H. S. Nwana.
Research and development challenges for agent-based systems.
IEE Proc. Softw. Eng., 144(1), 1997.
- 39
-
H. J. Ohlbach and R. A. Schmidt.
Functional translation and second-order frame properties of modal
logics.
J. Logic Computat., 7(5):581-603, 1997.
- 40
-
A. S. Rao.
Decision procedures for propositional linear-time
belief-desire-intention logics.
In Proc. ATAL'95, vol. 1037 of LNAI, pp. 102-118.
Springer, 1996.
- 41
-
A. S. Rao and M. P. Georgeff.
Modeling rational agents within a BDI-architecture.
In Proc. KR'91, pp. 473-484. Morgan Kaufmann, 1991.
- 42
-
R. A. Schmidt.
Optimised Modal Translation and Resolution.
PhD thesis, Univ. d. Saarlandes, Germany, 1997.
- 43
-
R. A. Schmidt.
12#12-unification for subsystems of S4.
In Proc. RTA'98, vol. 1379 of LNCS, pp. 106-120.
Springer, 1998.
- 44
-
R. A. Schmidt.
Decidability by resolution for propositional modal logics.
J. Automated Reasoning, 22(4):379-396, 1999.
- 45
-
R. A. Schmidt.
Relational grammars for knowledge representation.
To appear in Variable-Free Semantics, 1999.
- 46
-
W. van der Hoek.
Systems for knowledge and beliefs.
J. Logic Computat., 3(2):173-195, 1993.
- 47
-
B. van Linder, W. van der Hoek, and J.-J. C. Meyer.
Formalizing abilities and opportunities of agents.
Fundameta Informaticae, 34(1, 2):53-101, 1998.
- 48
-
F. Wolter.
Fusions of modal logics revisited.
In Advances in Modal Logic, Vol. 1, pp. 361-379. CSLI Publ.,
1998.
- 49
-
F. Wolter and M. Zakharyaschev.
Satisfiability problem in decsription logics with modal operators.
In Proc. KR-98, pp. 512-513. Morgan Kaufmann, 1998.
- 50
-
M. Wooldridge.
Agent-based computing.
Interoperable Comm. Networks, 1(1):71-97, 1998.
- 51
-
M. Wooldridge, C. Dixon, and M. Fisher.
A tableau-based proof method for temporal logics of knowledge and
belief.
J. Appl. Non-Classical Logics, 8(3):225-258, 1998.
- WP1
- The development of efficient proof methods for combinations of logics
with static interactions (on the proposional level), but
no dynamic interactions (between the modal operators).
- 1.1
- Examination of different theoretical specification
frameworks modelling intelligent agents and investigation of
common combinations of logics with no or very limited interaction.
- 1.2
- Specification of a translation approach, different basic proof methods
and strategies for theorem proving tasks via first-order, modal and
temporal resolution.
- 1.3
- Collection of examples to be used for testing the ideas and techniques
developed in subsequent workpages.
- 1.4
- Identification of non-trivial interactions with respect to relevant logical
properties (such as decidability, non first-order definability), which are
to receive special attention in WP2 and WP3.
Report due at the end of month 6.
- WP2
- The development of efficient proof methods, where possible decision
procedures, for combinations of modal logics
with non-trivial interactions identified in workpage WP1.
- 2.1
- Interacting epistemic and dynamic
modalities.
- 2.2
- Interacting epistemic and temporal
modalities.
- 2.3
- Investigation of the combination first-order resolution and
inductive reasoning needed for combinations with
dynamic and temporal logics.
Report due at the end of month 18.
- WP3
- The development of efficient proof methods, where possible decision
procedures, for combinations of first-order
and modal logics with non-trivial interactions.
- 3.1
- Interacting epistemic and
motivational operations.
- 3.2
- Interacting epistemic, dynamic, temporal and
motivational operations.
- 3.3
- Extraction of general combination principles.
Report due at the end of month 30.
- WP4
- Application of the developed methods to some simple case studies
from the literature, evaluation and comparison of the different
methods and strategies, and the development of a prototypical
implementation as an extension of an existing first-order theorem prover.
- 4.1
- Designing and implementing an input language
suitable for agent specifications, and translation to first-order logic.
- 4.2
- Implementing and testing of different proof strategies.
Final report and prototype proof system due at the end of month 36.
Copyright © 2001
Department of Computer Science, University of Manchester
Last modified: 2001-05-23
schmidt@cs.man.ac.uk

