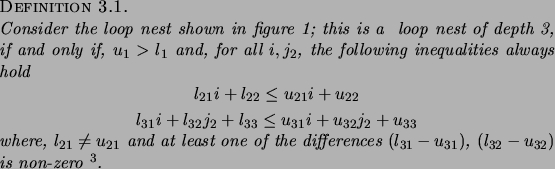 3
3
A subclass of the loop nests shown in figure 1 is defined as follows:
Definition 3.1 provides the basis for the following theorem.
|
In order to illustrate the results of Theorem 3.1,
consider the loop nest shown in figure 2. Assuming that
N  1, then the inequalities 3
1, then the inequalities 3 ![]() 2*I+1
and J+2
2*I+1
and J+2 ![]() 5*I always hold, while, for each inequality,
the coefficients
of I are non-zero; hence, the requirements of Definition 3.1
are satisfied and the loop nest is a canonical loop nest of depth 3.
Based on Theorem 3.1 and assuming that the
number of iterations of the outer loop, N, is a multiple of
5*I always hold, while, for each inequality,
the coefficients
of I are non-zero; hence, the requirements of Definition 3.1
are satisfied and the loop nest is a canonical loop nest of depth 3.
Based on Theorem 3.1 and assuming that the
number of iterations of the outer loop, N, is a multiple of ![]() ,
where
,
where ![]() is the number of processors,
partitioning the loop nest according to (4) leads to
perfect load balance.
is the number of processors,
partitioning the loop nest according to (4) leads to
perfect load balance.
To provide an intuitive view of this partitioning scheme,
the corresponding geometrical representation of the original
loop nest is shown in figure 3.a. Assuming
that two processors are used, the index of the outer loop
is partitioned into
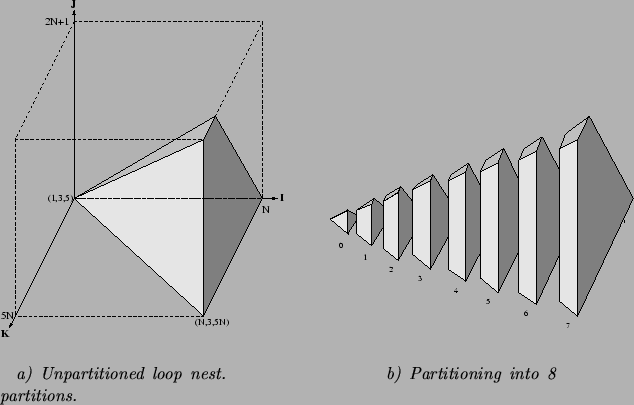 partitions;
the corresponding polytope for
each partition is shown in figure 3.b.
Then, applying (4), the first processor is assigned
partitions 0, 3, 5, and 6, while the second processor is assigned
partitions 1, 2, 4, and 7; in geometrical terms, the polytopes have
been assigned to two groups in such a way that the total volume
of the polytopes in each group is the same.
partitions;
the corresponding polytope for
each partition is shown in figure 3.b.
Then, applying (4), the first processor is assigned
partitions 0, 3, 5, and 6, while the second processor is assigned
partitions 1, 2, 4, and 7; in geometrical terms, the polytopes have
been assigned to two groups in such a way that the total volume
of the polytopes in each group is the same.
The partitioning
technique suggested in the proof of Theorem 3.1 can also
be applied when the number of iterations of the outer
loop, ![]() , is not a multiple of
, is not a multiple of ![]() ;
in this case, assuming that partitioning along the index of the outermost
loop is performed as evenly as possible (that is, each partition
has a number of iterations which differs by at most 1 from that of
any other partition), a small value of load imbalance is expected.
Theorem 3.1 can also be extended to cover cases where there
are more than one inner loops at the same level (i.e., loops which are
surrounded only by the same outer loops) whose bounds depend on the
index of a surrounding loop; the necessary requirement
is that, for any loop, the lower bound is always less than or
equal to the upper bound. Finally, in the general case, where
not all the inequalities in Definition 3.1 hold, index
set splitting can be applied to transform the original loop nest
into multiple adjacent loop nests, each of which satisfies the
requirements of Definition 3.1 [12].
;
in this case, assuming that partitioning along the index of the outermost
loop is performed as evenly as possible (that is, each partition
has a number of iterations which differs by at most 1 from that of
any other partition), a small value of load imbalance is expected.
Theorem 3.1 can also be extended to cover cases where there
are more than one inner loops at the same level (i.e., loops which are
surrounded only by the same outer loops) whose bounds depend on the
index of a surrounding loop; the necessary requirement
is that, for any loop, the lower bound is always less than or
equal to the upper bound. Finally, in the general case, where
not all the inequalities in Definition 3.1 hold, index
set splitting can be applied to transform the original loop nest
into multiple adjacent loop nests, each of which satisfies the
requirements of Definition 3.1 [12].