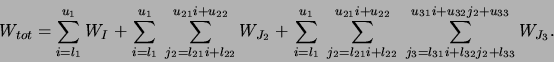The loop nests considered in this paper have the form shown in
figure 1. It is assumed that the sets of statements
labelled statements.1, statements.2, ![]() ,
statements.5 do not contain statements whose execution
depends on the value of the index of a surrounding loop;
hence, the workload corresponding to each set of statements
remains the same for any iteration of the outermost loop 2. It is also assumed
that the third set (statements.3) contains at least one
statement, i.e. it is not empty, while the remaining sets of statements
may be empty. The outermost loop, denoted by DOALL in the figure,
is parallel, that is, its iterations can run concurrently on different
processors.
,
statements.5 do not contain statements whose execution
depends on the value of the index of a surrounding loop;
hence, the workload corresponding to each set of statements
remains the same for any iteration of the outermost loop 2. It is also assumed
that the third set (statements.3) contains at least one
statement, i.e. it is not empty, while the remaining sets of statements
may be empty. The outermost loop, denoted by DOALL in the figure,
is parallel, that is, its iterations can run concurrently on different
processors.
Assuming that ![]() is the total amount of computation in the loop nest
which is distributed amongst
is the total amount of computation in the loop nest
which is distributed amongst ![]() processors in such a way that each processor
processors in such a way that each processor
![]() ,
, ![]() , is assigned an amount of computation equal to
, is assigned an amount of computation equal to ![]() (clearly,
(clearly,
![]() ), then we say that this
distribution exhibits a load imbalance,
), then we say that this
distribution exhibits a load imbalance, ![]() , equal to
, equal to
In order to compute the values of
![]() ,
we consider the computational work corresponding to each set
of statements of the loop body. Assume that
,
we consider the computational work corresponding to each set
of statements of the loop body. Assume that ![]() is the work
corresponding to the statements which are executed only by the
outermost loop (i.e., statements.1 and statements.5),
is the work
corresponding to the statements which are executed only by the
outermost loop (i.e., statements.1 and statements.5),
![]() is the work corresponding to the statements which are executed
by the loop with index
is the work corresponding to the statements which are executed
by the loop with index ![]() but not by the loop with index
but not by the loop with index ![]() (i.e.,
statements.2 and statements.4), and
(i.e.,
statements.2 and statements.4), and ![]() is the work
corresponding to the statements which are in the body of the loop with
index
is the work
corresponding to the statements which are in the body of the loop with
index ![]() (i.e., statements.3); then, the total amount of work
in the loop nest,
(i.e., statements.3); then, the total amount of work
in the loop nest, ![]() , is given by
, is given by