


Next: Partitioning for Load Balance
Up: Background
Previous: Load Imbalance
In the case of loops, an estimate for the values of 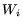 in (1)
can be derived by considering the number of times that each part of
the loop body is executed. This corresponds to the
problem of enumerating the integer points of a polytope, a
complicated problem for which it is not known whether a polynomial
algorithm exists [1]. In the context of loop nests,
some techniques to solve this problem are described in
[5,14,17].
in (1)
can be derived by considering the number of times that each part of
the loop body is executed. This corresponds to the
problem of enumerating the integer points of a polytope, a
complicated problem for which it is not known whether a polynomial
algorithm exists [1]. In the context of loop nests,
some techniques to solve this problem are described in
[5,14,17].
In general, counting the number of times, 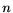 , that a statement surrounded
by
, that a statement surrounded
by 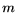 loops is executed can be computed by an expression of the form
loops is executed can be computed by an expression of the form
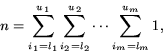 |
(3) |
where 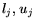 are the lower and upper bounds, respectively, of the
are the lower and upper bounds, respectively, of the
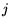 -th loop,
-th loop,
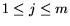 . Whenever, for each loop, the loop bounds
are constant, integer expressions, known at compile-time, it is trivial
to show that
. Whenever, for each loop, the loop bounds
are constant, integer expressions, known at compile-time, it is trivial
to show that
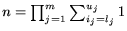 . However,
in a variety of situations, the loop bounds may be non-constant (for instance, dependent on the index
of an outer loop), or may contain expressions whose value is unknown
at compile-time. For the latter, the most important constraint
to respect when evaluating sums such as these in (3), is
whether the upper bound is greater than the lower bound. Considering
this may lead to different answers when symbolic bounds are involved.
In this paper, whenever this is the case, we split the loop iterations
in such a way that the upper bound is always greater than the lower
bound; this is discussed in Section 3.4.
. However,
in a variety of situations, the loop bounds may be non-constant (for instance, dependent on the index
of an outer loop), or may contain expressions whose value is unknown
at compile-time. For the latter, the most important constraint
to respect when evaluating sums such as these in (3), is
whether the upper bound is greater than the lower bound. Considering
this may lead to different answers when symbolic bounds are involved.
In this paper, whenever this is the case, we split the loop iterations
in such a way that the upper bound is always greater than the lower
bound; this is discussed in Section 3.4.



Next: Partitioning for Load Balance
Up: Background
Previous: Load Imbalance
Rizos Sakellariou
2000-07-31
![]() in (1)
can be derived by considering the number of times that each part of
the loop body is executed. This corresponds to the
problem of enumerating the integer points of a polytope, a
complicated problem for which it is not known whether a polynomial
algorithm exists [1]. In the context of loop nests,
some techniques to solve this problem are described in
[5,14,17].
in (1)
can be derived by considering the number of times that each part of
the loop body is executed. This corresponds to the
problem of enumerating the integer points of a polytope, a
complicated problem for which it is not known whether a polynomial
algorithm exists [1]. In the context of loop nests,
some techniques to solve this problem are described in
[5,14,17].
![]() , that a statement surrounded
by
, that a statement surrounded
by ![]() loops is executed can be computed by an expression of the form
loops is executed can be computed by an expression of the form